
����Ŀ���ŷ����Ǵ��ϲ����һ���˶��������������С�����������㳡�Ϸŷ��ݣ���ͼ������A����С���÷��ݹ�����һ�������ϣ����ݹ̶�����D������ʱ����AD��ˮƽ�ߵļн�Ϊ30�㣬Ϊ�˱��ڹ۲죬С��Ѹ����ǰ���ƶ������ߵ�������A��10��B������ʱ������BD��ˮƽ�ߵļн�Ϊ45�㣮��֪��A��B��C��ͬһ��ˮƽֱ���ϣ��������С����ʱ���ջصķ����ߵij����Ƕ����ף���������AD��BD��Ϊ�߶Σ� ![]() ��1.414��
��1.414�� ![]() ��1.732���������ȷ��1�ף���
��1.732���������ȷ��1�ף��� 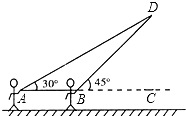
���𰸡��⣺��DH��BC��H����DH=x�ף� 
�ߡ�ACD=90�㣬
����ֱ�ǡ�ADH�У���DAH=30�㣬AD=2DH=2x��AH=DH��tan30��= ![]() x��
x��
��ֱ�ǡ�BDH�У���DBH=45�㣬BH=DH=x��BD= ![]() x��
x��
��AH��BH=AB=10�ף�
�� ![]() x��x=10��
x��x=10��
��x=5�� ![]() +1����
+1����
��С����ʱ���ջصķ��ݵij���Ϊ��
AD��BD=2x�� ![]() x=��2��
x=��2�� ![]() ����5��
����5�� ![]() +1���֣�2��1.414����5����1.732+1����8��
+1���֣�2��1.414����5����1.732+1����8��
����������DH��BC��H����DH=x�ף��������Ǻ�����ʾ��AH��BH�ij�������AH��BH=AB�õ�һ������x�ķ��̣��ⷽ�����x��ֵ���������AD��BD�ij������ɽ��⣮


 ��ѧ����ϵ�д�
��ѧ����ϵ�д� �ο�������ϵ�д�
�ο�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���ACB=90�㣬AC=BC��CD�ǡ�ACB�Ľ�ƽ���ߣ���E��F�ֱ��DZ�AC�� BC�ϵĶ��㣬AC=4����AE=x��BF=y��
��1����x+y=3�����ı���CEDF�������
��2����DE��DFʱ����ͼ2����̽��x��y֮���������ϵ��
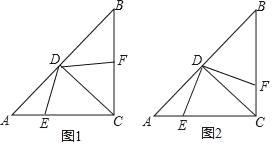
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����н�����̣���-15���£�![]() -3����6
-3����6
��������ԭʽ=��-15���£�-![]() ����6 ����һ����
����6 ����һ����
=��-15���£�-25�����ڶ�����
=-![]() ����������
����������
������⣺
���������������������һ���ǵ�______���������ԭ����______���ڶ����ǵ�______���������ԭ����______��
��������ȷ����⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����D��E��F�ֱ���AB��BC��AC���ϣ���BE=CF��BD=CE��
��1����֤����DEF�ǵ��������Σ�
��2������A=50��ʱ�����DEF�Ķ�����
��3������A=��DEF���жϡ�DEF�Ƿ�Ϊ����ֱ�������Σ�
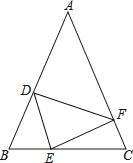
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧΪ������ѧϰ���������ļ�ֵ�ۣ��ضԱ�У����ѧ�������������������һ�����֪ʶ�IJ��ԣ��ɼ���ΪA��B��C��D��E������飬x��ʾ���Գɼ�����ͨ���Բ��Գɼ��ķ������õ���ͼ��ʾ��������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣮
A�飺90��x��100 B�飺80��x��90 C�飺70��x��80 D�飺60��x��70 E�飺x��60
��1���μӵ�����Ե�ѧ�������ˣ��뽫����ͳ��ͼ�������� ��
��2�����ε�����Գɼ�����λ���������ڣ�
��3�����ε�����Գɼ���80�����ϣ���80�֣�Ϊ���㣬����ѧ����3000�ˣ������ȫУ���Գɼ�Ϊ�����ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���A=100�㣬BI��CI�ֱ�ƽ�֡�ABC����ACB�����BIC=________����BM��CM�ֱ�ƽ�֡�ABC����ACB�����ƽ���ߣ����M=__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=(m+2)x+3-n��
(l)m��n�Ǻ�ֵʱ��y��x���������С��
(2)m��nΪ��ֵʱ��������ͼ��ԭ�㣿
(3)������ͼ���ڶ������������ޣ��� m��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���������Լ��ˮ��ij�жԾ�����ˮ�շ�ʵ�С�����ˮ�ۡ�����ÿ����ˮ��ͳ����������180�������IJ��ְ�ÿ������5Ԫ�շѣ�����180�����ײ�����260�����IJ��ְ�ÿ������7Ԫ�շѣ�����260�����IJ��ְ�ÿ������9Ԫ�շ�.
��1����ÿ����ˮ��Ϊx�����ף���������ˮ�ۡ�Ӧ��ˮ��yԪ����д��y(Ԫ)��x�������ף�֮��ĺ�������ʽ��
��2��������Ԥ��2015��ȫ����ˮ��Ϊ200����������ô��������ˮ�ۡ��շѣ�����Ӧ��ˮ�Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
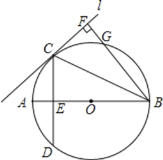
����Ŀ����ͼ��ʾ����֪AB��![]() ��ֱ����ֱ��L��
��ֱ����ֱ��L��![]() �����ڵ�C��
�����ڵ�C��![]() ��CD��AB��E��
��CD��AB��E��![]() ֱ��L������ΪF��BF��
ֱ��L������ΪF��BF��![]() ��C��
��C��
![]() ͼ�������߶���AE��ȣ���֤����Ľ��ۣ�
ͼ�������߶���AE��ȣ���֤����Ľ��ۣ�
![]() ��
��![]() ��
��![]() ����AB��ֵ��
����AB��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com