
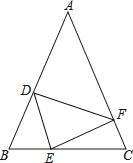
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数;
(3)若∠A=∠DEF,判断△DEF是否为等腰直角三角形.
【答案】(1)见解析;(2)∠DEF=65°;(3)△DEF不可能是等腰直角三角形.
【解析】
(1)根据AB=AC可得∠B=∠C,再利用“边角边”得到△BDE≌△CEF,即可得证;
(2)根据(1)中得到的全等三角形可得∠CEF=∠BDE,于是得到∠DEF=∠B,再根据等腰三角形的性质即可得解;
(3)由(1)知:△DEF是等腰三角形,即DE=EF,由(2)知,∠DEF=∠B,所以△DEF不可能为等腰直角三角形.
解:(1)∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
∵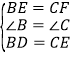 ,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE,
∵△BDE≌△CEF,
∴∠CEF=∠BDE,
∴∠DEF=∠B,
又∵在△ABC中,AB=AC,∠A=50°,
∴∠B=65°,
∴∠DEF=65°;
(3)由(1)知:△DEF是等腰三角形,即DE=EF,
由(2)知,∠DEF=∠B,
而∠B不可能为直角,
∴△DEF不可能是等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB.点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.

(1)若∠AEF=20°,∠ADE=50°,AC=2,求AB的长度;
(2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直尺的宽度为2cm,A、B两点在直尺的一条边上,AB=8cm,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为cm. 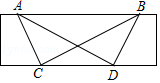
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数y=(k﹣3)x+k,给出下列结论:
①此函数是一次函数,
②无论k取什么值,函数图象必经过点(﹣1,3),
③若图象经过二、三、四象限,则k的取值范围是k<0,
④若函数图象与x轴的交点始终在正半轴可得k<3.其中正确的是( )
A. ①② B. ①③ C. ②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
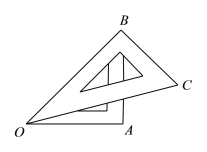
【题目】如图,将一幅三角板摆放在一起.
(1)∠AOC的度数为________,射线OA 、OB、OC组成所有小于平角的和为________;
(2)反向延长射线OA 到D,OE为∠BOD的平分线,OF为∠COD的平分线,请按题意画出图形,并求出∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段, ![]() ≈1.414,
≈1.414, ![]() ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米). 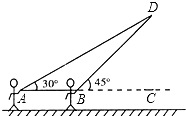
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 A=2 x2+3xy﹣2x﹣1,B= x2﹣xy﹣1.
(1)化简:4A﹣(2B+3A),将结果用含有 x、y 的式子表示;
(2)若式子 4A﹣(2B+3A)的值与字母 x 的取值无关,求 y3+![]() A﹣
A﹣ ![]() B 的值.
B 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com