
【题目】已知:如图,直尺的宽度为2cm,A、B两点在直尺的一条边上,AB=8cm,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为cm. 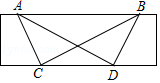
科目:初中数学 来源: 题型:
【题目】数列:0,2,4,8,12,18,…是我国的大衍数列,也是世界数学史上第一道数列题.该数列中的奇数项可表示为![]() ,偶数项表示为
,偶数项表示为![]() .
.
如:第一个数为![]() =0,第二个数为
=0,第二个数为![]() =2,…
=2,…
现在数轴的原点上有一点P,依次以大衍数列中的数为距离向左右来回跳跃.
第1秒时,点P在原点,记为P1;
第2秒时,点P向左跳2个单位,记为P2,此时点P2所表示的数为-2;
第3秒时,点P向右跳4个单位,记为P3,此时点P3所表示的数为2;
…
按此规律跳跃,点P20表示的数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,CD是∠ACB的角平分线,点E,F分别是边AC, BC上的动点,AC=4,设AE=x,BF=y.
(1)若x+y=3,求四边形CEDF的面积;
(2)当DE⊥DF时,如图2,试探索x、y之间的数量关系.
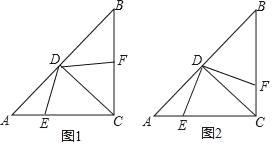
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题. 随着人们环保意识的增强及科学技术的进步,各种绿色环保新产品进入千家万户,今年一月份小楠家将天然气热水器换成了太阳能热水器,减少天然气的用量,去年12月份小楠家的天然气费一共是96元,从今年一月份起天然气费价格每立方米上涨了25%,小楠家2月份的用气量比去年12月份少10立方米,2月份的天然气费一共是90元,请你求小楠家今年2月份用气量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:(-15)÷(![]() -3)×6
-3)×6
(解析)原式=(-15)÷(-![]() )×6 (第一步)
)×6 (第一步)
=(-15)÷(-25)(第二步)
=-![]() (第三步)
(第三步)
解答问题:
①上面解答过程有两个错误,第一处是第______步,错误的原因是______;第二处是第______步,错误的原因是______;
②请你正确解答本题.
查看答案和解析>>
科目:初中数学 来源: 题型:
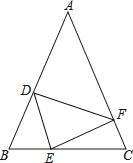
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数;
(3)若∠A=∠DEF,判断△DEF是否为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用水,某市对居民用水收费实行“阶梯水价”,按每年用水量统计,不超过180立方米的部分按每立方米5元收费;超过180立方米不超过260立方米的部分按每立方米7元收费;超过260立方米的部分按每立方米9元收费.
(1)设每年用水量为x立方米,按“阶梯水价”应缴水费y元,请写出y(元)与x(立方米)之间的函数解析式;
(2)明明家预计2015年全年用水量为200立方米,那么按“阶梯水价”收费,她家应缴水费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com