练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

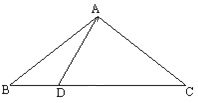
    【题目】已知：如图，△ABC中，AB=AC=10，BC=16，点D在BC上，DA⊥CA于A。

    求：BD的长。

    【答案】

    【解析】

    先根据等腰三角形的性质和勾股定理求出AE=6，设BD=x，则DE=8﹣x，DC=16﹣x．在Rt△ADE和Rt△ADC中利用勾股定理得：AD2=AE2+DE2=DC2﹣AC2，继而代入求出x的值即可．

    如图,过点A作AE⊥BC于点E，

    ∵AB=AC=10，BC=16，∴BE=CE=8，

    在Rt△ACE中，利用勾股定理可知：AE===6，

    设BD=x，则DE=8﹣x，DC=16﹣x，

    又DA⊥CA，

    在Rt△ADE和Rt△ADC中分别利用勾股定理得：AD2=AE2+DE2=DC2﹣AC2，

    代入为：62+（8﹣x）2=（16﹣x）2﹣102，解得：x=．

    即BD=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

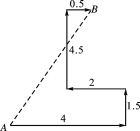
    【题目】如图，某人到岛上去探宝，从A处登陆后先往东走4 km，又往北走1.5 km，遇到障碍后又往西走2 km，再折回向北走到4.5 km处往东一拐，仅走0.5 km就找到宝藏．问登陆点A与宝藏埋藏点B之间的距离是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，长方形ABCD中，AB=4cm，BC=8cm．点P从点A出发，沿AB匀速运动；点Q从点C出发，沿C→B→A→D→C的路径匀速运动．两点同时出发，在B点处首次相遇后，点P的运动速度每秒提高了3cm，并沿B→C→D→A的路径匀速运动；点Q保持速度不变，继续沿原路径匀速运动，3s后两点在长方形ABCD某一边上的E点处第二次相遇后停止运动．设点P原来的速度为xcm/s.

    （1）点Q的速度为 cm/s（用含x的代数式表示）；

    　（2）求点P原来的速度．

    （3）判断E点的位置并求线段DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】温州苍南马站四季柚，声名远播，今年又是一个丰收年，某经销商为了打开销路，对1 000个四季柚进行打包优惠出售．打包方式及售价如图所示．假设用这两种打包方式恰好装完全部柚子．

    (1)若销售a箱纸盒装和a袋编织袋装四季柚的收入共950元，求a的值；

    (2)当销售总收入为7 280元时：

    ①若这批四季柚全部售完，请问纸盒装共包装了多少箱，编织袋装共包装了多少袋．

    ②若该经销商留下b(b>0)箱纸盒装送人，其余柚子全部售出，求b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

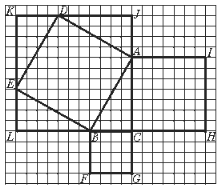
    【题目】在两千多年前我国古算术上记载有“勾三股四弦五”.你知道它的意思吗？

    它的意思是说：如果一个直角三角形的两条直角边长分别为3和4个长度单位，那么它的斜边的长一定是5个长度单位，而且3、4、5这三个数有这样的关系：32+42=52.

    （1）请你动动脑筋，能否验证这个事实呢？该如何考虑呢？

    （2）请你观察下列图形，直角三角形ABC的两条直角边的长分别为AC=7，BC=4，请你研究这个直角三角形的斜边AB的长的平方是否等于42+72？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，直尺的宽度为2cm，A、B两点在直尺的一条边上，AB=8cm，C、D两点在直尺的另一条边上．若∠ACB=∠ADB=90°，则C、D两点之间的距离为cm．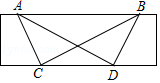

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两名同学进行登山比赛，图中表示甲、乙两人沿相同的路线同时从山脚出发，各自离山脚的距离随时间变化的图象，根据图象中的有关数据回答下列问题：

    （1）分别求出表示甲、乙两同学登山过程中离山脚的距离h（千米）与时间t（时）的函数表达式；

    （2）当甲到达山顶时，乙行进到山路上的某点A处，求A点距山顶的距离；

    （3）在（2）的条件下，设乙同学从A点继续登山，甲同学到达山顶后游玩小时，沿原路下山，在点B处与乙同学相遇，此时点B与山顶距离为1千米，相遇后甲、乙各自沿原路下山和上山，求乙到达山顶时，甲离山脚的距离是多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一幅三角板摆放在一起．

    （1）∠AOC的度数为________，射线OA 、OB、OC组成所有小于平角的和为________；

    （2）反向延长射线OA 到D，OE为∠BOD的平分线，OF为∠COD的平分线，请按题意画出图形，并求出∠EOF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：为了求1+3+32+33+…+3100的值，可设M=1+3+32+33+…+3100，则3M=3+32+33+34+…+3101，因此3M﹣M=3101﹣1．所以M=，即1+3+32+33+…+3100=．问题解决：仿照上述方法求下列式子的值．

    （1）1+4+42+43+…+420．

    （2）5101+5102+5103+…+52018．

    查看答案和解析>>

    同步练习册答案