
【题目】折叠矩形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
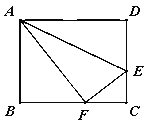
【答案】3cm
【解析】
要求CE的长,就必须求出DE的长,如果设EC=x,那么我们可将DE,EC转化到一个三角形中进行计算,根据折叠的性质我们可得出AD=AF,DE=EF,那么DE,CE就都转化到直角三角形EFC中了,下面的关键就是求出FC的长,也就必须求出BF的长,我们发现直角三角形ABF中,已知了AB的长,AF=AD=10,因此可求出BF的长,也就有了CF的长,在直角三角形EFC中,可用勾股定理,得出关于x的一元二次方程,进而求出未知数的值.
依题意可得:BC=AD=AF=10,DE=EF.
在△ABF中,∠ABF=90°,∴![]() ,∴FC=10﹣6=4,
,∴FC=10﹣6=4,
设EC=x,则EF=DE=8﹣x.
∵∠C=90°,∴EC2+FC2=EF2,∴x2+42=(8﹣x)2,
解得:x=3,∴EC=3(cm).


科目:初中数学 来源: 题型:
【题目】如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB.点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.

(1)若∠AEF=20°,∠ADE=50°,AC=2,求AB的长度;
(2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则∠AOB的度数是( )

A. 25° B. 30° C. 35° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州苍南马站四季柚,声名远播,今年又是一个丰收年,某经销商为了打开销路,对1 000个四季柚进行打包优惠出售.打包方式及售价如图所示.假设用这两种打包方式恰好装完全部柚子.
(1)若销售a箱纸盒装和a袋编织袋装四季柚的收入共950元,求a的值;
(2)当销售总收入为7 280元时:
①若这批四季柚全部售完,请问纸盒装共包装了多少箱,编织袋装共包装了多少袋.
②若该经销商留下b(b>0)箱纸盒装送人,其余柚子全部售出,求b的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直尺的宽度为2cm,A、B两点在直尺的一条边上,AB=8cm,C、D两点在直尺的另一条边上.若∠ACB=∠ADB=90°,则C、D两点之间的距离为cm. 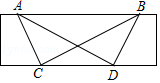
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数y=(k﹣3)x+k,给出下列结论:
①此函数是一次函数,
②无论k取什么值,函数图象必经过点(﹣1,3),
③若图象经过二、三、四象限,则k的取值范围是k<0,
④若函数图象与x轴的交点始终在正半轴可得k<3.其中正确的是( )
A. ①② B. ①③ C. ②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 A=2 x2+3xy﹣2x﹣1,B= x2﹣xy﹣1.
(1)化简:4A﹣(2B+3A),将结果用含有 x、y 的式子表示;
(2)若式子 4A﹣(2B+3A)的值与字母 x 的取值无关,求 y3+![]() A﹣
A﹣ ![]() B 的值.
B 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com