
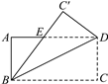
【题目】如图所示,将长方形ABCD沿直线BD折叠,使点C落在点C′处,BC′交AD于点E,AD=16,AB=8,求DE的长.
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】某车间有60个工人,生产甲、乙两种零件,每人每天平均能生产甲种零件24个或乙种零件12个.已知每2个甲种零件和3个乙种零件配成一套,问应分配多少人生产甲种零件,多少人生产乙种零件,才能使每天生产的这两种零件刚好配套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家庭过期药品属于“国家危险废物“处理不当将污染环境,危害健康.某市药监部门为了了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如图:
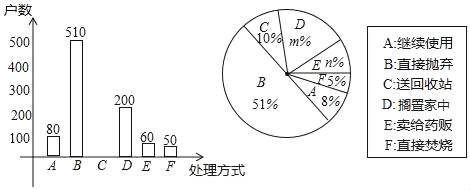
(1)求m、n的值;
(2)补全条形统计图;
(3)家庭过期药品的正确处理方式是送回收站,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,请你观察下列几种简单多面体模型,解答下列问题:

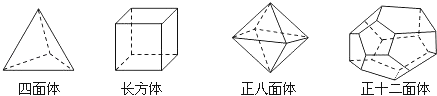
图1 图2
(探索新知)如图1,(1)根据上面多面体模型,完成表格中的空格;
多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
四面体 | 4 | 4 | |
长方体 | 8 | 6 | 12 |
正八面体 | 8 | 12 | |
正十二面体 | 20 | 12 | 30 |
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .
(2)根据以上关系式猜想是否存在一个多面体,它有16个面,50条棱,34个顶点?并写出理由。
(实际应用)如图2,足球一般有32块黑白皮子缝合而成,黑色的是正五边形,白色的是正六边形,如
果我们近似把足球看成一个多面体.
(1)设黑色的正五边形有x块,则白色的正六边形有(32﹣x)块,当把足球看成一个多面体时,它的棱数是 ,它的顶点数是 .
(2)求出黑皮和白皮各有多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数列:0,2,4,8,12,18,…是我国的大衍数列,也是世界数学史上第一道数列题.该数列中的奇数项可表示为![]() ,偶数项表示为
,偶数项表示为![]() .
.
如:第一个数为![]() =0,第二个数为
=0,第二个数为![]() =2,…
=2,…
现在数轴的原点上有一点P,依次以大衍数列中的数为距离向左右来回跳跃.
第1秒时,点P在原点,记为P1;
第2秒时,点P向左跳2个单位,记为P2,此时点P2所表示的数为-2;
第3秒时,点P向右跳4个单位,记为P3,此时点P3所表示的数为2;
…
按此规律跳跃,点P20表示的数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A,B对应的数分别为-4,8.
(1)如图1,如果点P和点Q分别从点A,点B同时出发,沿数轴负方向运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒6个单位.
① 求A,B两点之间的距离.
② 当P,Q两点相遇时,点P在数轴上对应的数几.
③ 求点P出发多少秒后,与点Q之间相距4个单位长度?
(2)如图2,如果点P从点A出发沿数轴的正方向以每秒2个单位的速度运动,点Q从点B出发沿数轴的负方向以每秒6个单位的速度运动,点M从数轴原点O出发沿数轴的正方向以每秒1个单位的速度运动,若三个点同时出发,经过多少秒后有MP=MQ?
![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com