
【题目】已知数轴上两点A,B对应的数分别为-4,8.
(1)如图1,如果点P和点Q分别从点A,点B同时出发,沿数轴负方向运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒6个单位.
① 求A,B两点之间的距离.
② 当P,Q两点相遇时,点P在数轴上对应的数几.
③ 求点P出发多少秒后,与点Q之间相距4个单位长度?
(2)如图2,如果点P从点A出发沿数轴的正方向以每秒2个单位的速度运动,点Q从点B出发沿数轴的负方向以每秒6个单位的速度运动,点M从数轴原点O出发沿数轴的正方向以每秒1个单位的速度运动,若三个点同时出发,经过多少秒后有MP=MQ?
![]()
![]()
【答案】(1)①12,②-10,③点P出发2秒或者4秒后,与点Q之间相距4个单位长度;(2)经过![]() 或
或![]() 秒后,有MP=MQ.
秒后,有MP=MQ.
【解析】
(1)①根据两点间的距离公式即可求解;
②根据相遇时间=路程差÷速度差先求出时间,再根据路程=速度×时间求解即可;
③分两种情况:P,Q两点相遇前;P,Q两点相遇后;进行讨论即可求解;
(2)分两种情况:M在P,Q两点之间;P,Q两点相遇;进行讨论即可求解.
(1)①A,B两点之间的距离为8﹣(﹣4)=12.
②12÷(6﹣2)=3(秒),﹣4﹣2×3=﹣10.
故当P,Q两点相遇时,点P在数轴上对应的数是﹣10.
③P,Q两点相遇前,(12﹣4)÷(6﹣2)=2(秒);
P,Q两点相遇后,(12+4)÷(6﹣2)=4(秒).
故求点P出发2或4秒后,与点Q之间相距4个单位长度;
(2)设三个点同时出发,经过t秒后有MP=MQ,M在P,Q两点之间,8﹣6t﹣t=t﹣(﹣4+2t),解得:t![]() ;
;
P,Q两点相遇,2t+6t=12,解得:t![]() .
.
故若三个点同时出发,经过![]() 或
或![]() 秒后有MP=MQ.
秒后有MP=MQ.
故答案为:12;﹣10.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】除夕夜,父母给自己的一双儿女发压岁钱,先每人发了200元,然后在三个红包里面分别装有标有100元,300元,500元的卡片,每个红包和卡片除数字不同外,其余均相同,妹妹从三个红包中随机抽取了一个红包,记录数字后放回洗匀,哥哥再随机抽取一个红包,请用列表法或画树状图的方法,求父母给自己的一双儿女发压岁钱总和大于800元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边,A为直角顶点,在AD左侧作等腰直角三角形ADF,连接CF,AB=AC,∠BAC=90°.
(1)当点D在线段BC上时(不与点B重合),线段CF和BD的数量关系与位置关系分别是什么?请给予证明.
(2)当点D在线段BC的延长线上时,(1)的结论是否仍然成立?请在图2中画出相应的图形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求画图,并回答问题.
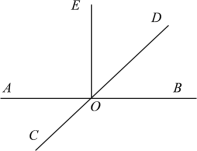
已知:直线AB,CD相交于点O,且OE⊥AB.
(1)过点O画直线MN⊥CD;
(2)若点F是(1)中所画直线MN上任意一点(O点除外),若∠AOC=35°,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桐梓县“四抓四到位”确保教育均衡发展,加速城区新、扩建项目工程,加快建设某间小学,公司经过调查了解:甲、乙两个工程队有能力承包建校工程,甲工程队单独完成建校工程的时间是乙工程队的2倍,甲、乙两队合作完成建校工程需要60天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)若甲、乙两队共同工作了10天后,乙队因其他工作停止施工,由甲队单独继续施工,要使甲队总的工作量不少于乙队已做工作量的2倍,那么甲队至少再单独施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB.点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.

(1)若∠AEF=20°,∠ADE=50°,AC=2,求AB的长度;
(2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则∠AOB的度数是( )

A. 25° B. 30° C. 35° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数y=(k﹣3)x+k,给出下列结论:
①此函数是一次函数,
②无论k取什么值,函数图象必经过点(﹣1,3),
③若图象经过二、三、四象限,则k的取值范围是k<0,
④若函数图象与x轴的交点始终在正半轴可得k<3.其中正确的是( )
A. ①② B. ①③ C. ②③ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com