
【题目】桐梓县“四抓四到位”确保教育均衡发展,加速城区新、扩建项目工程,加快建设某间小学,公司经过调查了解:甲、乙两个工程队有能力承包建校工程,甲工程队单独完成建校工程的时间是乙工程队的2倍,甲、乙两队合作完成建校工程需要60天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)若甲、乙两队共同工作了10天后,乙队因其他工作停止施工,由甲队单独继续施工,要使甲队总的工作量不少于乙队已做工作量的2倍,那么甲队至少再单独施工多少天?
【答案】(1)甲工程队单独完成建校工程需要180天,乙工程队单独完成建校工程需要90天(2)甲队至少再单独施工30天
【解析】
(1)根据题意可设乙工程队单独完成建校工程需要x天,则甲工程队单独完成建校工程需要2x天,利用甲乙合作工作量之和等于1,可列方程:60![]() =1,
=1,
解得:x=90,所以2x=180.
(2)根据题意可设甲队再单独施工y天,
然后根据题意得:![]() ,解得:y≥30.
,解得:y≥30.
(1)设乙工程队单独完成建校工程需要x天,则甲工程队单独完成建校工程需要2x天,
根据题意得:60(![]() +
+![]() )=1,
)=1,
解得:x=90,
经检验,x=90是原方程的解,且符合题意,
∴2x=180.
答:甲工程队单独完成建校工程需要180天,乙工程队单独完成建校工程需要90天.
(2)设甲队再单独施工y天,
根据题意得:![]() ≥
≥![]() ×2,
×2,
解得:y≥30,
答:甲队至少再单独施工30天.


科目:初中数学 来源: 题型:
【题目】如图①,底面积为30cm2的空圆柱容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②. 
(1)求圆柱形容器的高和匀速注水的水流速度;
(2)若“几何体”的下方圆柱的底面积为15cm2 , 求“几何体”上方圆柱体的高和底面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司员工分别住在A、B、C三个住宅区,A区有25人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应设在( )
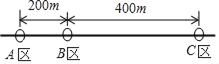
A. A区 B. B区 C. A区或B区 D. C区
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A,B对应的数分别为-4,8.
(1)如图1,如果点P和点Q分别从点A,点B同时出发,沿数轴负方向运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒6个单位.
① 求A,B两点之间的距离.
② 当P,Q两点相遇时,点P在数轴上对应的数几.
③ 求点P出发多少秒后,与点Q之间相距4个单位长度?
(2)如图2,如果点P从点A出发沿数轴的正方向以每秒2个单位的速度运动,点Q从点B出发沿数轴的负方向以每秒6个单位的速度运动,点M从数轴原点O出发沿数轴的正方向以每秒1个单位的速度运动,若三个点同时出发,经过多少秒后有MP=MQ?
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某容器由A、B、C三个连通长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是整个容器容积的![]() (容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(1)求注满整个容器所需的总时间;
(2)设容器A的高度为xcm,则容器B的高度为 cm;
(3)求容器A的高度和注水的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y= ![]() (x<0)的图象经过点A,若S△ABO=
(x<0)的图象经过点A,若S△ABO= ![]() ,则k的值为 .
,则k的值为 . 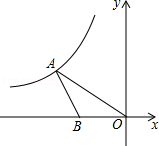
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE. 
(1)求证:BC是⊙O的切线;
(2)若tan∠G= ![]() ,BE=4,求⊙O的半径;
,BE=4,求⊙O的半径;
(3)在(2)的条件下,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b=;
(2)补全频数分布直方图;
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表该市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com