
【题目】根据要求画图,并回答问题.
已知:直线AB,CD相交于点O,且OE⊥AB.
(1)过点O画直线MN⊥CD;
(2)若点F是(1)中所画直线MN上任意一点(O点除外),若∠AOC=35°,求∠EOF的度数.
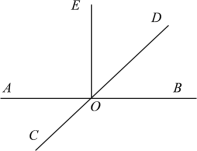
【答案】(1)如图所示见解析;(2)∠EOF的度数为35°或145°.
【解析】
(1)根据题意画出直线MN即可;
(2)当F在OM上时,根据垂直定义求出∠EOF=∠BOD,根据对顶角求出∠EOF=∠AOC,即可求出答案;当F在ON上时,求出∠AOM的度数,根据对顶角求出∠BON的度数,求出∠EOB+∠BON即可.
(1)如图所示:
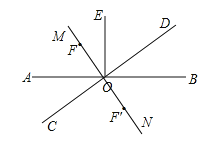
(2)如上图:①当F在OM上时.
∵EO⊥AB,MN⊥CD,∴∠EOB=∠MOD=90°,∴∠MOE+∠EOD=90°,∠EOD+∠BOD=90°,∴∠EOF=∠BOD=∠AOC=35°;
②当F在ON上时,如图在F′点时.
∵MN⊥CD,∴∠MOC=90°=∠AOC+∠AOM,∴∠AOM=90°﹣∠AOC=55°,∴∠BON=∠AOM=55°,∴∠EOF′=∠EOB+∠BON=90°+55°=145°.
答:∠EOF的度数是35°或145°.


科目:初中数学 来源: 题型:
【题目】在长方形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD﹣AB=2时,S2﹣S1的值为_______.(用a、b的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,请你观察下列几种简单多面体模型,解答下列问题:

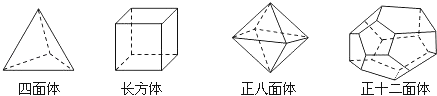
图1 图2
(探索新知)如图1,(1)根据上面多面体模型,完成表格中的空格;
多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
四面体 | 4 | 4 | |
长方体 | 8 | 6 | 12 |
正八面体 | 8 | 12 | |
正十二面体 | 20 | 12 | 30 |
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .
(2)根据以上关系式猜想是否存在一个多面体,它有16个面,50条棱,34个顶点?并写出理由。
(实际应用)如图2,足球一般有32块黑白皮子缝合而成,黑色的是正五边形,白色的是正六边形,如
果我们近似把足球看成一个多面体.
(1)设黑色的正五边形有x块,则白色的正六边形有(32﹣x)块,当把足球看成一个多面体时,它的棱数是 ,它的顶点数是 .
(2)求出黑皮和白皮各有多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数列:0,2,4,8,12,18,…是我国的大衍数列,也是世界数学史上第一道数列题.该数列中的奇数项可表示为![]() ,偶数项表示为
,偶数项表示为![]() .
.
如:第一个数为![]() =0,第二个数为
=0,第二个数为![]() =2,…
=2,…
现在数轴的原点上有一点P,依次以大衍数列中的数为距离向左右来回跳跃.
第1秒时,点P在原点,记为P1;
第2秒时,点P向左跳2个单位,记为P2,此时点P2所表示的数为-2;
第3秒时,点P向右跳4个单位,记为P3,此时点P3所表示的数为2;
…
按此规律跳跃,点P20表示的数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A,B对应的数分别为-4,8.
(1)如图1,如果点P和点Q分别从点A,点B同时出发,沿数轴负方向运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒6个单位.
① 求A,B两点之间的距离.
② 当P,Q两点相遇时,点P在数轴上对应的数几.
③ 求点P出发多少秒后,与点Q之间相距4个单位长度?
(2)如图2,如果点P从点A出发沿数轴的正方向以每秒2个单位的速度运动,点Q从点B出发沿数轴的负方向以每秒6个单位的速度运动,点M从数轴原点O出发沿数轴的正方向以每秒1个单位的速度运动,若三个点同时出发,经过多少秒后有MP=MQ?
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,CD是∠ACB的角平分线,点E,F分别是边AC, BC上的动点,AC=4,设AE=x,BF=y.
(1)若x+y=3,求四边形CEDF的面积;
(2)当DE⊥DF时,如图2,试探索x、y之间的数量关系.
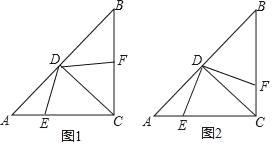
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:(-15)÷(![]() -3)×6
-3)×6
(解析)原式=(-15)÷(-![]() )×6 (第一步)
)×6 (第一步)
=(-15)÷(-25)(第二步)
=-![]() (第三步)
(第三步)
解答问题:
①上面解答过程有两个错误,第一处是第______步,错误的原因是______;第二处是第______步,错误的原因是______;
②请你正确解答本题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com