
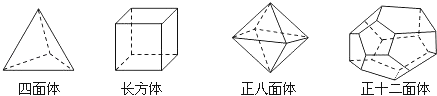
ЁОЬтФПЁПЪЎАЫЪРМЭШ№ЪПЪ§бЇМвХЗРжЄУїСЫМђЕЅЖрУцЬхжаЖЅЕуЪ§ЃЈVЃЉЁЂУцЪ§ЃЈFЃЉЁЂРтЪ§ЃЈEЃЉжЎМфДцдкЕФвЛИігаШЄЕФЙиЯЕЪНЃЌЧыФуЙлВьЯТСаМИжжМђЕЅЖрУцЬхФЃаЭЃЌНтД№ЯТСаЮЪЬтЃК

ЭМ1 ЭМ2
ЃЈЬНЫїаТжЊЃЉШчЭМ1ЃЌЃЈ1ЃЉИљОнЩЯУцЖрУцЬхФЃаЭЃЌЭъГЩБэИёжаЕФПеИёЃЛ
ЖрУцЬх | ЖЅЕуЪ§ЃЈVЃЉ | УцЪ§ЃЈFЃЉ | РтЪ§ЃЈEЃЉ |
ЫФУцЬх | 4 | 4 | |
ГЄЗНЬх | 8 | 6 | 12 |
е§АЫУцЬх | 8 | 12 | |
е§ЪЎЖўУцЬх | 20 | 12 | 30 |
ФуЗЂЯжЖЅЕуЪ§ЃЈVЃЉЁЂУцЪ§ЃЈFЃЉЁЂРтЪ§ЃЈEЃЉжЎМфДцдкЕФЙиЯЕЪНЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉИљОнвдЩЯЙиЯЕЪНВТЯыЪЧЗёДцдквЛИіЖрУцЬхЃЌЫќга16ИіУцЃЌ50ЬѕРтЃЌ34ИіЖЅЕуЃПВЂаДГіРэгЩЁЃ
ЃЈЪЕМЪгІгУЃЉШчЭМ2ЃЌзуЧђвЛАуга32ПщКкАзЦЄзгЗьКЯЖјГЩЃЌКкЩЋЕФЪЧе§ЮхБпаЮЃЌАзЩЋЕФЪЧе§СљБпаЮЃЌШч
ЙћЮвУЧНќЫЦАбзуЧђПДГЩвЛИіЖрУцЬхЃЎ
ЃЈ1ЃЉЩшКкЩЋЕФе§ЮхБпаЮгаxПщЃЌдђАзЩЋЕФе§СљБпаЮгаЃЈ32ЉxЃЉПщЃЌЕБАбзуЧђПДГЩвЛИіЖрУцЬхЪБЃЌЫќЕФРтЪ§ЪЧ ЁЁЃЌЫќЕФЖЅЕуЪ§ЪЧ ЁЁЃЎ
ЃЈ2ЃЉЧѓГіКкЦЄКЭАзЦЄИїгаЖрЩйПщЃП
ЁОД№АИЁПЁОЬНЫїаТжЊЁПЃЈ1ЃЉ6,6ЃЌV+FЉE=2ЃЛ(2)ВЛДцдкЃЛ
ЁОЪЕМЪгІгУЁПЃЈ1ЃЉЉ![]() x+96ЃЌЃЛЉ
x+96ЃЌЃЛЉ![]() x+64ЃЌЃЈ2ЃЉе§ЮхБпаЮга12ПщЃЌе§СљБпаЮга20ПщЃЎ
x+64ЃЌЃЈ2ЃЉе§ЮхБпаЮга12ПщЃЌе§СљБпаЮга20ПщЃЎ
ЁОНтЮіЁП
ЬНЫїаТжЊЃЈ1ЃЉЙлВьЭМаЮМДПЩЕУГіНсТлЃЛЙлВьПЩЕУЖЅЕуЪ§+УцЪ§-РтЪ§=2ЃЛ
ЃЈ2ЃЉДњШыЃЈ1ЃЉжаЕФЪНзгМДПЩбщжЄ.
ЪЕМЪгІгУЃЈ1ЃЉжБНгРћгУХЗРЙЋЪНЧѓГіД№АИЃЛ
ЃЈ2ЃЉИљОнЬтвтПЩжЊЃКБОЬтжаЕФЕШСПЙиЯЕЪЧЁАКкАзЦЄПщ32ПщЁБКЭвђЮЊУППщАзЦЄга3ЬѕБпгыКкБпСЌдквЛЦ№ЃЌЫљвдКкЦЄжЛгаЃЈ32-xЃЉПщЃЌЖјКкЦЄЙВгаБпЪ§ЮЊ5xПщЃЌвРДЫНшжњХЗРЙЋЪНСаЗНГЬЧѓНтМДПЩЃЎ
ЬНЫїаТжЊЃЈ1ЃЉЙлВьБэИёПЩвдПДГіЃКЖЅЕуЪ§+УцЪ§РтЪ§=2ЃЌЙиЯЕЪНЮЊЃКV+FE=2ЃЛ
ЖрУцЬх | ЖЅЕуЪ§(V) | УцЪ§(F) | РтЪ§(E) |
ЫФУцЬх | 4 | 4 | 6 |
ГЄЗНЬх | 8 | 6 | 12 |
е§АЫУцЬх | 6 | 8 | 12 |
е§ЪЎЖўУцЬх | 20 | 12 | 30 |
ЃЈ2ЃЉгЩЬтвтжЊЃЌV=34ЃЌF=16ЃЌE=50ЃЌВЛЗћКЯЙиЯЕЪНЃКV+FE=2.ЙЪУЛгаетбљЕФЖрБпаЮ.
ЪЕМЪгІгУЃЈ1ЃЉЩше§ЮхБпаЮгаxПщЃЌдђе§СљБпаЮга32xПщЃЌ
дђF=32,E=5x+![]() =
= ![]() x+96
x+96
V=EЁТ3ЁС2=![]() +64
+64
ЃЈ2ЃЉИљОнХЗРЙЋЪНЕУЃКV+FE=2ЃЌ
дђ![]() x+64+32(
x+64+32(![]() x+96)=2ЃЌ
x+96)=2ЃЌ
НтЕУЃКx=12ЃЌ32x=20ЃЌ
ЫљвдЃЌе§ЮхБпаЮга/span>12ПщЃЌе§СљБпаЮга20Пщ.


 ШЋгХЕуСЗЕЅдЊМЦЛЎЯЕСаД№АИ
ШЋгХЕуСЗЕЅдЊМЦЛЎЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
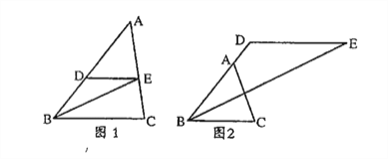
ЁОЬтФПЁПЁїABCжаЃЌDЪЧABБпЩЯЕФвЛЕуЃЌЙ§ЕуDзїDEЁЮBCЃЌЁЯABCЕФНЧЦНЗжЯпгкЕуE.
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуEЧЁКУдкACБпЩЯЪБЃЌЧѓжЄЃКЁЯADE=2ЁЯDEBЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуDдкBAЕФбгГЄЯпЩЯЪБЃЌЦфгрЬѕМўВЛБфЃЌЧыжБНгаДГіЁЯADEгыЁЯDEBжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯABCКЭЁЯACBЕФЦНЗжЯпЯрНЛгкЕуFЃЌЙ§FзїDEЁЮBCЃЌНЛABгкЕуDЃЌНЛACгкЕуEЃЎШєBD=4ЃЌDE=7ЃЌдђЯпЖЮECЕФГЄЮЊЃЈЁЁЁЁЃЉ

A. 3 B. 4 C. 3.5 D. 2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌШ§НЧаЮABCЃЈМЧзїЁїABCЃЉдкЗНИёжаЃЌЗНИёжНжаЕФУПИіаЁЗНИёЖМЪЧБпГЄЮЊ1ИіЕЅЮЛЕФе§ЗНаЮЃЌШ§ИіЖЅЕуЕФзјБъЗжБ№ЪЧAЃЈЉ2ЃЌ1ЃЉЃЌBЃЈЉ3ЃЌЉ2ЃЉЃЌCЃЈ1ЃЌЉ2ЃЉЃЌЯШНЋЁїABCЯђЩЯЦНвЦ3ИіЕЅЮЛГЄЖШЃЌдйЯђгвЦНвЦ2ИіЕЅЮЛГЄЖШЃЌЕУЕНA1B1C1ЃЎ
ЃЈ1ЃЉдкЭМжаЛГіЁїA1B1C1ЃЛ
ЃЈ2ЃЉЕуA1ЃЌB1ЃЌC1ЕФзјБъЗжБ№ЮЊЁЁ ЁЁЁЂЁЁ ЁЁЁЂЁЁ ЁЁЃЛ
ЃЈ3ЃЉШєyжсгавЛЕуPЃЌЪЙЁїPBCгыЁїABCУцЛ§ЯрЕШЃЌЧѓГіPЕуЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћЪТМўAЗЂЩњЕФИХТЪЪЧ ![]() ЃЌФЧУДдкЯрЭЌЬѕМўЯТжиИДЪдбщЃЌЯТСа4жжГТЪіжаЃЌВЛе§ШЗЕФга ЂйЫЕУїзі100ДЮетжжЪдбщЃЌЪТМўAБиЗЂЩњ1ДЮ
ЃЌФЧУДдкЯрЭЌЬѕМўЯТжиИДЪдбщЃЌЯТСа4жжГТЪіжаЃЌВЛе§ШЗЕФга ЂйЫЕУїзі100ДЮетжжЪдбщЃЌЪТМўAБиЗЂЩњ1ДЮ
ЂкЫЕУїЪТМўAЗЂЩњЕФЦЕТЪЪЧ ![]()
ЂлЫЕУїзі100ДЮетжжЪдбщжаЃЌЧА99ДЮЪТМўAУЛЗЂЩњЃЌКѓ1ДЮЪТМўAВХЗЂЩњ
ЂмЫЕУїзі100ДЮетжжЪдбщЃЌЪТМўAПЩФмЗЂЩњ1ДЮЃЈ ЃЉ
A.ЂйЁЂЂкЁЂЂл
B.ЂйЁЂЂкЁЂЂм
C.ЂкЁЂЂлЁЂЂм
D.ЂйЁЂЂкЁЂЂлЁЂЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
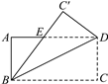
ЁОЬтФПЁПШчЭМЫљЪОЃЌНЋГЄЗНаЮABCDбижБЯпBDелЕўЃЌЪЙЕуCТфдкЕуCЁфДІЃЌBCЁфНЛADгкЕуEЃЌADЃН16ЃЌABЃН8ЃЌЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
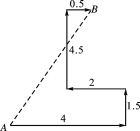
ЁОЬтФПЁПШчЭМЃЌФГШЫЕНЕКЩЯШЅЬНБІЃЌДгAДІЕЧТНКѓЯШЭљЖЋзп4 kmЃЌгжЭљББзп1.5 kmЃЌгіЕНеЯАКѓгжЭљЮїзп2 kmЃЌдйелЛиЯђББзпЕН4.5 kmДІЭљЖЋвЛЙеЃЌНізп0.5 kmОЭевЕНБІВиЃЎЮЪЕЧТНЕуAгыБІВиТёВиЕуBжЎМфЕФОрРыЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИљОнвЊЧѓЛЭМЃЌВЂЛиД№ЮЪЬтЃЎ
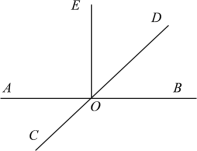
вбжЊЃКжБЯпABЃЌCDЯрНЛгкЕуOЃЌЧвOEЁЭABЃЎ
ЃЈ1ЃЉЙ§ЕуOЛжБЯпMNЁЭCDЃЛ
ЃЈ2ЃЉШєЕуFЪЧЃЈ1ЃЉжаЫљЛжБЯпMNЩЯШЮвтвЛЕу(OЕуГ§Эт)ЃЌШєЁЯAOCЃН35ЁуЃЌЧѓЁЯEOFЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮТжнВдФЯТэеОЫФМОшжЃЌЩљУћдЖВЅЃЌНёФъгжЪЧвЛИіЗсЪеФъЃЌФГОЯњЩЬЮЊСЫДђПЊЯњТЗЃЌЖд1 000ИіЫФМОшжНјааДђАќгХЛнГіЪлЃЎДђАќЗНЪНМАЪлМлШчЭМЫљЪОЃЎМйЩшгУетСНжжДђАќЗНЪНЧЁКУзАЭъШЋВПшжзгЃЎ
(1)ШєЯњЪлaЯфжНКазАКЭaДќБржЏДќзАЫФМОшжЕФЪеШыЙВ950дЊЃЌЧѓaЕФжЕЃЛ
(2)ЕБЯњЪлзмЪеШыЮЊ7 280дЊЪБЃК
ЂйШєетХњЫФМОшжШЋВПЪлЭъЃЌЧыЮЪжНКазАЙВАќзАСЫЖрЩйЯфЃЌБржЏДќзАЙВАќзАСЫЖрЩйДќЃЎ
ЂкШєИУОЯњЩЬСєЯТb(b>0)ЯфжНКазАЫЭШЫЃЌЦфгршжзгШЋВПЪлГіЃЌЧѓbЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com