
【题目】家庭过期药品属于“国家危险废物“处理不当将污染环境,危害健康.某市药监部门为了了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如图:
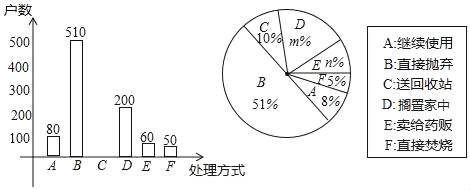
(1)求m、n的值;
(2)补全条形统计图;
(3)家庭过期药品的正确处理方式是送回收站,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站.
【答案】(1)m=20,n=6;(2)见解析;(3)18万户.
【解析】
(1)首先根据A类有80户,占8%,求出抽样调査的家庭总户数,再用D类户数除以总户数求出m,用E类户数除以总户数求出n;
(2)用总户数分别减去A、B、D、E、F类户数,得到C类户数,即可补全条形统计图;
(3)用180万户乘以样本中送回收点的户数所占百分比即可.
(1)∵抽样调査的家庭总户数为:80÷8%=1000(户),
∴m%=![]() =20%,m=20,
=20%,m=20,
n%=![]() =6%,n=6.
=6%,n=6.
(2)C类户数为:1000﹣(80+510+200+60+50)=100,
条形统计图补充如下:
(3)180×10%=18(万户).
若该市有180万户家庭,估计大约有18万户家庭处理过期药品的方式是送回收点.


科目:初中数学 来源: 题型:
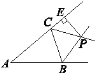
【题目】如图,△ABC的两条外角平分线BP,CP相交于点P,PE⊥AC交AC的延长线于点E.若△ABC的周长为11,PE=2,S△BPC=2,则S△ABC=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AB=6cm,D为边AB中点.动点P、Q在边AB上同时从点D出发,点P沿D→A以1cm/s的速度向终点A运动.点Q沿D→B→D以2cm/s的速度运动,回到点D停止.以PQ为边在AB上方作等边三角形PQN.将△PQN绕QN的中点旋转180°得到△MNQ.设四边形PQMN与△ABC重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<3).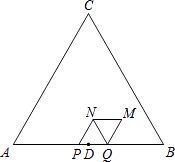
(1)当点N落在边BC上时,求t的值.
(2)当点N到点A、B的距离相等时,求t的值.
(3)当点Q沿D→B运动时,求S与t之间的函数表达式.
(4)设四边形PQMN的边MN、MQ与边BC的交点分别是E、F,直接写出四边形PEMF与四边形PQMN的面积比为2:3时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】除夕夜,父母给自己的一双儿女发压岁钱,先每人发了200元,然后在三个红包里面分别装有标有100元,300元,500元的卡片,每个红包和卡片除数字不同外,其余均相同,妹妹从三个红包中随机抽取了一个红包,记录数字后放回洗匀,哥哥再随机抽取一个红包,请用列表法或画树状图的方法,求父母给自己的一双儿女发压岁钱总和大于800元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=4,DE=7,则线段EC的长为( )

A. 3 B. 4 C. 3.5 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
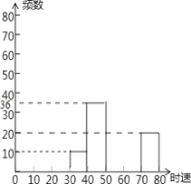
【题目】某路段某时段用雷达测速仪随机监测了200辆汽车的时速,得到如下频数分布表(不完整):注:30﹣40为时速大于或等于30千米而小于40千米,其它类同.
数据段 | 频数 |
30~40 | 10 |
_______ | 36 |
50~60 | 80 |
60~70 | _____ |
70~80 | 20 |
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果此路段该时间段经过的车有1000辆.估计约有多少辆车的时速大于或等于 60千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB.点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.

(1)若∠AEF=20°,∠ADE=50°,AC=2,求AB的长度;
(2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com