
【题目】如图,函数y= ![]() 与y=﹣kx+1(k≠0)在同一直角坐标系中的图象大致为( )
与y=﹣kx+1(k≠0)在同一直角坐标系中的图象大致为( )
A.
B.
C.
D.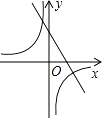
【答案】B
【解析】解:k>0时,一次函数y=﹣kx+1的图象经过第一、二、四象限,反比例函数的两个分支分别位于第一、三象限,选项B符合; k<0时,一次函数y=﹣kx+1的图象经过第一、二、三象限,反比例函数的两个分支分别位于第二、四象限,无选项符合.
故选:B.
【考点精析】通过灵活运用一次函数的图象和性质和反比例函数的图象,掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数;
(3)若∠A=∠DEF,判断△DEF是否为等腰直角三角形.
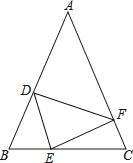
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用水,某市对居民用水收费实行“阶梯水价”,按每年用水量统计,不超过180立方米的部分按每立方米5元收费;超过180立方米不超过260立方米的部分按每立方米7元收费;超过260立方米的部分按每立方米9元收费.
(1)设每年用水量为x立方米,按“阶梯水价”应缴水费y元,请写出y(元)与x(立方米)之间的函数解析式;
(2)明明家预计2015年全年用水量为200立方米,那么按“阶梯水价”收费,她家应缴水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们运用图(Ⅰ)中大正方形的面积可表示为(a+b)2,也可表示为c3+4(![]() ab),即(a+b)2=c2+4(
ab),即(a+b)2=c2+4(![]() ab)由此推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
ab)由此推导出一个重要的结论a2+b2=c2,这个重要的结论就是著名的“勾股定理”.这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
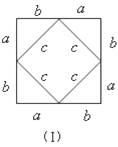
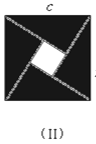
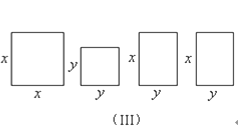
(1)请你用图(Ⅱ)(2002年国际数学家大会会标)的面积表达式验证勾股定理(其中四个直角三角形的较大的直角边长都为a,较小的直角边长都为b,斜边长都为c).
(2)请你用(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+2y)2=x2+4xy+4y2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:为了求1+3+32+33+…+3100的值,可设M=1+3+32+33+…+3100,则3M=3+32+33+34+…+3101,因此3M﹣M=3101﹣1.所以M=![]() ,
,
即1+3+32+33+…+3100=![]() .问题解决:仿照上述方法求下列式子的值.
.问题解决:仿照上述方法求下列式子的值.
(1)1+4+42+43+…+420.
(2)5101+5102+5103+…+52016.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知:
中,已知:![]() ,
,![]() ,
,![]() ,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转
,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转![]() 得到
得到![]() ,则旋转前后两个直角三角形重叠部分的面积为______
,则旋转前后两个直角三角形重叠部分的面积为______![]() .
.
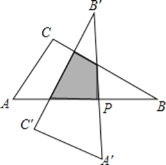
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AB是![]() 的直径,直线L与
的直径,直线L与![]() 相切于点C,
相切于点C,![]() ,CD交AB于E,
,CD交AB于E,![]() 直线L,垂足为F,BF交
直线L,垂足为F,BF交![]() 于C.
于C.
![]() 图中哪条线段与AE相等?试证明你的结论;
图中哪条线段与AE相等?试证明你的结论;
![]() 若
若![]() ,
,![]() ,求AB的值.
,求AB的值.
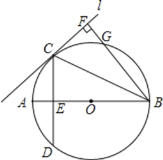
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 ![]() (其中
(其中 ![]() )与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
(1)求抛物线的关系式;
(2)过点 ![]() 的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com