
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E. 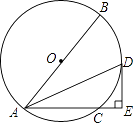
(1)求证:DE是⊙O的切线.
(2)求DE的长.
【答案】
(1)证明:连接OD,
∵AD平分∠BAC,
∴∠DAE=∠DAB,
∵OA=OD,∴∠ODA=∠DAO,
∴∠ODA=∠DAE,
∴OD∥AE,
∵DE⊥AC,
∴OD⊥DE,
∴DE是⊙O切线
(2)解:O作OF⊥AC于点F,
∴AF=CF=3,
∴OF= ![]() =
= ![]() =4.
=4.
∵∠OFE=∠DEF=∠ODE=90°,
∴四边形OFED是矩形,
∴DE=OF=4.

【解析】(1)连接OD,欲证明DE是⊙O的切线,只要证明OD⊥DE即可.(2)过点O作OF⊥AC于点F,只要证明四边形OFED是矩形即可得到DE=OF,在RT△AOF中利用勾股定理求出OF即可.
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】请仔细阅读下面材料,然后解决问题:
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”.例如: ![]() ,
, ![]() ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如: ![]() ,
, ![]() .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如: ![]() ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如: ![]() .
.
(1)将分式![]() 化为带分式;
化为带分式;
(2)当x取哪些整数值时,分式![]() 的值也是整数?
的值也是整数?
(3)当x的值变化时,分式![]() 的最大值为 .
的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AB=7 cm,AC=25 cm.点P从点A沿AB方向以1 cm/s的速度运动至点B,点Q从点B沿BC方向以6 cm/s的速度运动至点C,P,Q两点同时出发.
(1)求BC的长;
(2)当点P,Q运动2 s时,求P,Q两点之间的距离;
(3)P,Q两点运动几秒时,AP=CQ?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
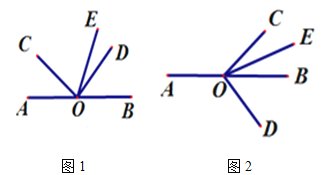
【题目】点O是直线AB上一点,∠COD是直角,OE平分∠BOC.
(1)①、如图1,若∠AOC=50°,求∠DOE的度数;
②、如图1,若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);
(2)将图1中的∠COD按顺时针方向旋转至图2所示的位置.
探究∠AOC与∠DOE的度数之间的关系,写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:

①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金秋十月,长沙市某中学组织七年级学生去某综合实践基地进行秋季社会实践活动,每人需购买一张门票,该综合实践基地的门票价格为每张240元,如果一次购买500张以上(不含500张)门票,则门票价格为每张220元,请回答下列问题:
(1)列式表示n个人参加秋季社会实践活动所需钱数;
(2)某校用132000元可以购买多少张门票;
(3)如果我校490人参加秋季社会实践,怎样购买门票花钱最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
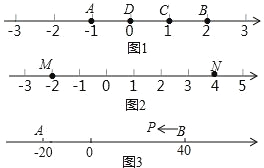
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
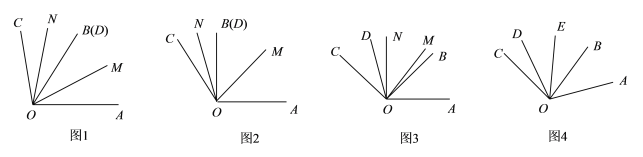
【题目】已知,如图1,∠AOB和∠COD共顶点O,OB和OD重合,OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β.
(1)如图2,若α=90°,β=30°,则∠MON=________;
(2)若将∠COD绕O逆时针旋转至图3的位置,求∠MON;(用α,β表示)
(3)如图4,若α=2β,∠COD绕O逆时针旋转,转速为3°/秒,∠AOB绕O同时逆时针旋转,转速为1°/秒(转到OC与OA共线时停止运动),且OE平分∠BOD,请判断∠COE与∠AOD的数量关系并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com