
【题目】如图,在Rt△ABC中,∠B=90°,AB=7 cm,AC=25 cm.点P从点A沿AB方向以1 cm/s的速度运动至点B,点Q从点B沿BC方向以6 cm/s的速度运动至点C,P,Q两点同时出发.
(1)求BC的长;
(2)当点P,Q运动2 s时,求P,Q两点之间的距离;
(3)P,Q两点运动几秒时,AP=CQ?

【答案】(1)BC=24 cm;(2)PQ=13 cm;(3)P,Q两点运动![]() s时,AP=CQ.
s时,AP=CQ.
【解析】
(1)在Rt△ABC中,∠B=90°,AB=7 cm,AC=25 cm根据勾股定理可得BC2=AC2-AB2=252-72=242,求出BC=24 cm.
(2)连接PQ,由题意知BP=7-2=5(cm),BQ=6×2=12(cm),在Rt△BPQ中,由勾股定理得:
PQ=BP2+BQ2=52+122=132,进而求出PQ=13 cm.
(3)设P,Q两点运动t s时,AP=CQ,则可得t=24-6t,解得t=![]() .
.
解:(1)∵在Rt△ABC中,∠B=90°,AB=7 cm,AC=25 cm
∴BC2=AC2-AB2=252-72=242,
∴BC=24 cm.
(2)连接PQ,
由题意知BP=7-2=5(cm),BQ=6×2=12(cm),
在Rt△BPQ中,由勾股定理,得:
PQ=BP2+BQ2=52+122=132,
∴PQ=13 cm.
(3)设P,Q两点运动t s时,
AP=CQ,则t=24-6t,
解得t=![]() .
.
答:P,Q两点运动![]() s时,AP=CQ.
s时,AP=CQ.


科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AD是BC边上的高,∠BDE=∠CDF=30°,在下列结论中:①△ABD≌△ACD;②2DE=2DF=AD;③△ADE≌△ADF;④4BE=4CF=AB.正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区计划对面积为400m2的区域进行绿化.经测算,甲队每天能完成绿化面积是乙队每天能完成绿化面积的2倍,且甲队单独完成比乙队单独完成少用4天.求甲、乙两队每天单独完成绿化的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果事件A发生的概率是 ![]() ,那么在相同条件下重复试验,下列4种陈述中,不正确的有 ①说明做100次这种试验,事件A必发生1次
,那么在相同条件下重复试验,下列4种陈述中,不正确的有 ①说明做100次这种试验,事件A必发生1次
②说明事件A发生的频率是 ![]()
③说明做100次这种试验中,前99次事件A没发生,后1次事件A才发生
④说明做100次这种试验,事件A可能发生1次( )
A.①、②、③
B.①、②、④
C.②、③、④
D.①、②、③、④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上点A对应的数是20,点B对应的数是﹣30,甲从A点出发以每秒1个单位长度的速度匀速运动,乙从B出发以每秒3个长度单位的速度匀速运动,若甲乙两人同时出发
(1)若甲和乙在数轴上运动3秒后,
①它们相距最远时,甲所在的位置对应的数是 ,乙所在的位置对应的数是
②它们距离最近时,甲所在的位置对应的数是 ,乙所在的位置对应的数是
(2)若甲和乙同时向右,出发多少秒后,甲和乙相距20个长度单位?
(3)若甲和乙进行匀速往返跑训练,甲从A点起跑,到达B点后,立即转身跑向A点,到达A点后,又立即转身跑向B点……;乙从B点起跑,到达A点后,立即转身跑向B点,到达B点后,又立即转身跑向A点……;两人同时出发,问:起跑后两人第二次相遇的时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人到岛上去探宝,从A处登陆后先往东走4 km,又往北走1.5 km,遇到障碍后又往西走2 km,再折回向北走到4.5 km处往东一拐,仅走0.5 km就找到宝藏.问登陆点A与宝藏埋藏点B之间的距离是多少?
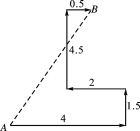
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆的半径为![]() 个单位长度.数轴上每个数字之间的距离为1个单位长度,在圆的4等分点处分别标上点A,B,C,D.先让圆周上的点A与数轴上表示-1的点重合.
个单位长度.数轴上每个数字之间的距离为1个单位长度,在圆的4等分点处分别标上点A,B,C,D.先让圆周上的点A与数轴上表示-1的点重合.
(1)圆的周长为多少?
(2)若该圆在数轴上向右滚动2周后,则与点A重合的点表示的数为多少?
(3)若将数轴按照顺时针方向绕在该圆上,(如数轴上表示-2的点与点B重合,数轴上表示-3的点与点C重合…),那么数轴上表示-2018的点与圆周上哪个点重合?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E. 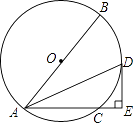
(1)求证:DE是⊙O的切线.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在两千多年前我国古算术上记载有“勾三股四弦五”.你知道它的意思吗?
它的意思是说:如果一个直角三角形的两条直角边长分别为3和4个长度单位,那么它的斜边的长一定是5个长度单位,而且3、4、5这三个数有这样的关系:32+42=52.
(1)请你动动脑筋,能否验证这个事实呢?该如何考虑呢?
(2)请你观察下列图形,直角三角形ABC的两条直角边的长分别为AC=7,BC=4,请你研究这个直角三角形的斜边AB的长的平方是否等于42+72?
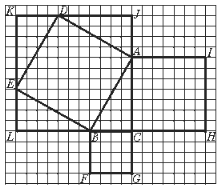
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com