Question

【题目】已知：点O到△ABC的两边AB、AC所在直线的距离OD=OE，且OB＝OC.

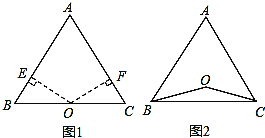
（1）如图，若点O在BC上，求证：AB＝AC；

（2）如图，若点O在△ABC的内部，求证：AB＝AC；

（3）若点O在△ABC的外部，AB＝AC成立吗？请画图表示.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析：（1）求证AB=AC，就是求证∠B=∠C，可通过构建全等三角形来求．过点O分别作OE⊥AB于E，OF⊥AC于F，那么可以用斜边直角边定理（HL）证明Rt△OEB≌Rt△OFC来实现；（2）首先得出Rt△OEB≌Rt△OFC，进而得出AB=AC；（3）不一定成立，当∠A的平分线所在直线与边BC的垂直平分线重合时，有AB=AC；否则，AB≠AC．

试题解析：（1）证明：过点O分别作OE⊥AB于E，OF⊥AC于F，

由题意知，

在Rt△OEB和Rt△OFC中

∴Rt△OEB≌Rt△OFC（HL），

∴∠ABC=∠ACB，

∴AB=AC；

（2）证明：过点O分别作OE⊥AB于E，OF⊥AC于F，

由题意知，OE=OF．∠BEO=∠CFO=90°，

∵在Rt△OEB和Rt△OFC中

∴Rt△OEB≌Rt△OFC（HL），

∴∠OBE=∠OCF，

又∵OB=OC，

∴∠OBC=∠OCB，

∴∠ABC=∠ACB，

∴AB=AC；

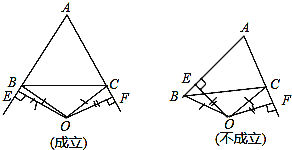
（3）不一定成立，当∠A的平分线所在直线与边BC的垂直平分线重合时AB=AC，否则AB≠AC．（如图）