Question

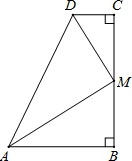
如图，在四边形ABCD中，∠B=∠C=90°，∠DAB与∠ADC的平分线相交于BC边上的M点，则下列结论：①∠AMD=90°；②M为BC的中点；③AB+CD=AD；④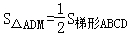；⑤M到AD的距离等于BC的一半；其中正确的有(     )

A．2个  B．3个   C．4个  D．5个

Answer 1

D【考点】全等三角形的判定与性质；角平分线的性质．

【分析】过M作ME⊥AD于E，得出∠MDE=∠CDA，∠MAD=∠BAD，求出∠MDA+∠MAD=（∠CDA+∠BAD）=90°，根据三角形内角和定理求出∠AMD，即可判断①；根据角平分线性质求出MC=ME，ME=MB，即可判断②和⑤；由勾股定理求出DC=DE，AB=AE，即可判断③；根据SSS证△DEM≌△DCM，推出S_三角形DEM=S_三角形DCM，同理得出S_三角形AEM=S_三角形ABM，即可判断④．

【解答】解：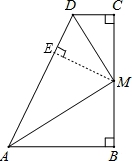

过M作ME⊥AD于E，

∵∠DAB与∠ADC的平分线相交于BC边上的M点，

∴∠MDE=∠CDA，∠MAD=∠BAD，

∵DC∥AB，

∴∠CDA+∠BAD=180°，

∴∠MDA+∠MAD=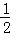（∠CDA+∠BAD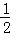）=×180°=90°，

∴∠AMD=180°﹣90°=90°，∴①正确；

∵DM平分∠CDE，∠C=90°（MC⊥DC），ME⊥DA，

∴MC=ME，

同理ME=MB，

∴MC=MB=ME=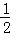BC，∴②正确；

∴M到AD的距离等于BC的一半，∴⑤正确；

∵由勾股定理得：DC²=MD²﹣MC²，DE²=MD²﹣ME²，

又∵ME=MC，MD=MD，

∴DC=DE，

同理AB=AE，

∴AD=AE+DE=AB+DC，∴③正确；

∵在△DEM和△DCM中

，

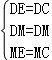∴△DEM≌△DCM（SSS），

∴S_三角形DEM=S_三角形DCM

同理S_三角形AEM=S_三角形ABM，

∴S_三角形AMD=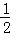S_梯形ABCD，∴④正确；

故选D．

【点评】本题考查了角平分线性质，垂直定义，直角梯形，勾股定理，全等三角形的性质和判定等知识点的应用，主要考查学生运用定理进行推理的能力．