
分析 (1)先化简根号内的数,再根据二次根式的乘法进行计算即可解答本题;
(2)先对原式化简,再合并同类项即可解答本题;
(3)先化简括号内的式子,再根据二次根式的除法进行计算即可;
(4)根据平方差公式、零指数幂、负整数指数幂进行计算即可.
解答 解:(1)$-\sqrt{3}•\sqrt{(-16)(-36)}$
=$-\sqrt{3}×\sqrt{16×36}$
=-$\sqrt{3}×24$
=-$24\sqrt{3}$;
(2)$a\sqrt{\frac{3}{a}}+\sqrt{9a}-\frac{{3\sqrt{a}}}{{\sqrt{3}}}$
=$\sqrt{3a}+3\sqrt{a}-\sqrt{3a}$
=$3\sqrt{a}$;
(3)(3$\sqrt{12}$-2$\sqrt{\frac{1}{3}}$+$\sqrt{48}$)÷2$\sqrt{3}$
=$(6\sqrt{3}-\frac{2\sqrt{3}}{3}+4\sqrt{3})÷2\sqrt{3}$
=$\frac{28\sqrt{3}}{3}×\frac{1}{2\sqrt{3}}$
=$\frac{14}{3}$;
(4)($\sqrt{3}$+1)($\sqrt{3}$-1)+($\sqrt{2}$-1)0-(-$\frac{1}{3}$)-2
=3-1+1-9
=-6.
点评 本题考查二次根式的混合运算、零指数幂、负整数指数幂,解题的关键是明确它们各自的计算方法,明确二次根式混合运算的计算方法.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量 | 200 | 200+10x | 800-200-(200+10x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
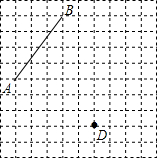 作图并回答问题.
作图并回答问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 每天使用零花钱数 | 1 | 2 | 3 | 5 | 6 |
| 人数 | 2 | 5 | 4 | 3 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
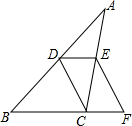 如图,在△ABC中,D、E分别是边AB、AC的中点,延长BC至点F,使得CF=$\frac{1}{2}$BC,连结CD、DE、EF.
如图,在△ABC中,D、E分别是边AB、AC的中点,延长BC至点F,使得CF=$\frac{1}{2}$BC,连结CD、DE、EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com