
(本题6分)在下列四个条件中:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.请
选出两个作为条件,得出△AED是等腰三角形(写出一个即可),并加以证明.
已知: ▲ ;
求证:△AED是等腰三角形.
证明:
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
(本题6分)在下列四个条件中:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.请
选出两个作为条件,得出△AED是等腰三角形(写出一个即可),并加以证明.

已知: ▲ ;
求证:△AED是等腰三角形.
证明:
【解析】根据全等三角形的判定和性质求证
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省温州地区初三适应性考试数学卷(解析版) 题型:解答题
(本题6分)在下列四个条件中:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.请
选出两个作为条件,得出△AED是等腰三角形(写出一个即可),并加以证明.
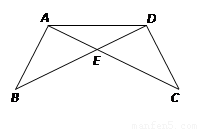
已知: ▲ ;
求证:△AED是等腰三角形.
证明:
【解析】根据全等三角形的判定和性质求证
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com