
如图,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C.
(1)求A、B、C三点的坐标.
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
(3)在 轴上方的抛物线上是否存在一点M,过M作MG
轴上方的抛物线上是否存在一点M,过M作MG
 轴于点G,使以A、M、G三点为顶点的三角形与
轴于点G,使以A、M、G三点为顶点的三角形与 PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
(1) A(-1,0),B(1,0),C(0,-1);(2)4;(3)(-2,3),(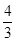 ,
,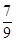 ),(4,15).
),(4,15).
解析试题分析:(1)抛物线与x轴的交点,即当y=0,C点坐标即当x=0,分别令y以及x为0求出A,B,C坐标的值;
(2)四边形ACBP的面积=△ABC+△ABP,由A,B,C三点的坐标,可知△ABC是直角三角形,且AC=BC,则可求出△ABC的面积,根据已知可求出P点坐标,可知AP的长度,以及点B到直线的距离,从而求出△ABP的面积,则就求出四边形ACBP的面积;
(3)假设存在这样的点M,两个三角形相似,根据题意以及上两题可知,∠PAC∠和∠MGA是直角,只需证明 或
或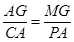 即可.设M点坐标,根据题中所给条件可求出线段AG,CA,MG,CA的长度,然后列等式,分情况讨论,求解.
即可.设M点坐标,根据题中所给条件可求出线段AG,CA,MG,CA的长度,然后列等式,分情况讨论,求解.
试题解析: (1)令y=0,
得x2-1=0
解得x=±1,
令x=0,得y=-1
∴A(-1,0),B(1,0),C(0,-1);
(2)∵OA=OB=OC=1,
∴∠BAC=∠ACO=∠BCO=45°.
∵AP∥CB,
∴∠PAB=45°.
过点P作PE⊥x轴于E,则△APE为等腰直角三角形,
令OE=A,则PE=A+1,
∴P(A,A+1).
∵点P在抛物线y=x2-1上,
∴A+1=A2-1.
解得A1=2,A2=-1(不合题意,舍去).
∴PE=3.
∴四边形ACBP的面积S= AB•OC+
AB•OC+ AB•PE=
AB•PE= ×2×1+
×2×1+ ×2×3=4;
×2×3=4;
(3)假设存在
∵∠PAB=∠BAC=45°,
∴PA⊥AC
∵MG⊥x轴于点G,
∴∠MGA=∠PAC=90°
在Rt△AOC中,OA=OC=1,
∴AC=
在Rt△PAE中,AE=PE=3,
∴AP=3
设M点的横坐标为m,则M(m,m2-1)
①点M在y轴左侧时,则m<-1.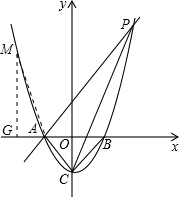
(ⅰ)当△AMG∽△PCA时,有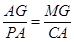 .
.
∵AG=-m-1,MG=m2-1.
即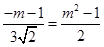
解得m1=-1(舍去)m2=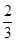 (舍去).
(舍去).
(ⅱ)当△MAG∽△PCA时有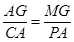 ,
,
即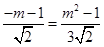 .
.
解得:m=-1(舍去)m2=-2.
∴M(-2,3)(10分).
②点M在y轴右侧时,则m>1
(ⅰ)当△AMG∽△PCA时有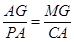
∵AG=m+1,MG=m2-1
∴
解得m1=-1(舍去)m2=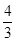 .
.
∴M(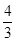 ,
,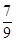 ).
).
(ⅱ)当△MAG∽△PCA时有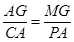 ,
,
即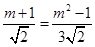 .
.
解得:m1=-1(舍去)m2=4,
∴M(4,15).
∴存在点M,使以A、M、G三点为顶点的三角形与△PCA相似
M点的坐标为(-2,3),(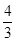 ,
,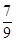 ),(4,15).
),(4,15).
考点: 二次函数综合题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:解答题
函数y =ax²(a≠0)与直线y =2x-3的图像交于点(1,b).
求:(1)a和b的值;
(2)求抛物线y =ax²的开口方向、对称轴、顶点坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线y=x+3与坐标轴分别交于A,B两点,抛物线y=ax2+bx-3a经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.
(1)求抛物线的解析式及顶点C的坐标;
(2)求证:四边形ABCD是直角梯形.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.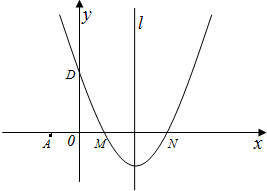
(1)求该抛物线的解析式.
(2)若过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式.
(3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完,该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润y1(元)与国内销售数量x(千件)的关系为:y1= 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=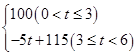
(1)用x的代数式表示t,则t=__________;当0<x≤3时,y2与x的函数关系式为:y2=__________________;当3≤x<________时,y2=100;
(2)当3≤x<6时,求每年该公司销售这种健身产品的总利润w(千元)与国内的销售数量x(千件)的函数关系式,并求此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知在平面直角坐标系中,四边形ABCO是梯形,且BC∥AO,其中A(6,0),B(3, ),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).
),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).

(1)求点C的坐标及梯形ABCO的面积;
(2)当点Q在CO边上运动时,求△OPQ的面积S与运动时间t的函数关系式,并写出自变量t的取值范围;
(3)以O,P,Q为顶点的三角形能构成直角三角形吗?若能,请求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3)。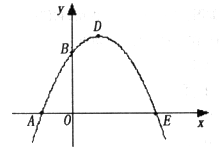
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积;
(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知二次函数 的图象经过点A(2,-3),B(-1,0).
的图象经过点A(2,-3),B(-1,0).
(1)求二次函数的解析式;
(2)观察函数图象,要使该二次函数的图象与 轴只有一个交点,应把图象沿
轴只有一个交点,应把图象沿 轴向上平移几个单位?
轴向上平移几个单位?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com