
 ��ͼ����ֱ������ϵ�У���֪A��0��a����B��b��0����C��b��c�����㣬����a��b��c�����ϵʽ��|a+b-5|+$\sqrt{2a-b-1}$=0����c-4��2��0��
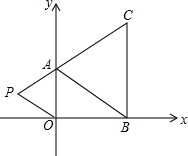
��ͼ����ֱ������ϵ�У���֪A��0��a����B��b��0����C��b��c�����㣬����a��b��c�����ϵʽ��|a+b-5|+$\sqrt{2a-b-1}$=0����c-4��2��0������ ��1�����ݡ������Ǹ�����ӣ���Ϊ0�����������Ǹ�����ֵΪ0�����з��̽��a��b��c��ֵ��
��2�����ݡ�ABQ������ǡ�ABC�����$\frac{1}{2}$�����ǵõ�BQ=$\frac{1}{2}$BC��������ý��ۣ�
��3����a��b��c��ֵ��������Ĺ�ʽ���г���ʽ�����m��ֵ��������P�����꼴�ɣ�
��� �⣺��1����|a+b-5|+$\sqrt{2a-b-1}$=0����c-4��2��0��
��a+b-5=0��2a-b-1=0��c-4=0��
��a=2��b=3��c=4��
��2���ߡ�ABQ������ǡ�ABC�����$\frac{1}{2}$��
��BQ=$\frac{1}{2}$BC��
��Q��3��2����3��-2����
��3����a=2��b=3��c=4��
���ABC�ĸ���������Ϊ��A��0��2����B��3��0����C��3��4����
��S��ABC=$\frac{1}{2}$��4��3=6��
��SABOP=S��APO+S��ABO=$\frac{1}{2}$��AO��|m|+$\frac{1}{2}$��AO��OB=$\frac{1}{2}$��2|m|+$\frac{1}{2}$��2��3=|m|+3=6�����ı���ABOP��������ABC�������ȣ�
��|m|=3��m=��3��
���ڵڶ���������һ��P��m��$\frac{1}{2}$����
��P��-3��$\frac{1}{2}$����
���� ���⿼���˵�������ȷ�����Ǹ��������ʣ��������Ŀʱ�ɸ��ݷǸ��������ʷֱ������������ֵ���ٸ��������ȼ��ɵó��𰸣��������Ŀʱ�̽�������ͼ�β�����������εĺͣ��ٽ��м��㼴�ɣ�


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
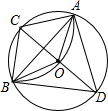 ��ͼ��CDΪ��Oֱ������C��ΪԲ�ģ�COΪ�뾶����������O��A��B���㣬��֤��AD=BD=BA��
��ͼ��CDΪ��Oֱ������C��ΪԲ�ģ�COΪ�뾶����������O��A��B���㣬��֤��AD=BD=BA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
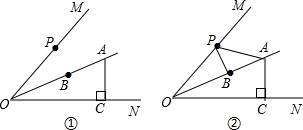
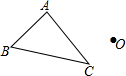 ��ͼ����֪��ABC�͡�ABC��һ��O������A��B��C��ʹ�����ABC���ڵ�O�����ĶԳƣ�
��ͼ����֪��ABC�͡�ABC��һ��O������A��B��C��ʹ�����ABC���ڵ�O�����ĶԳƣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
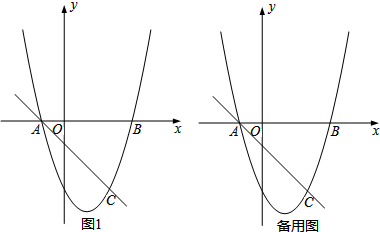
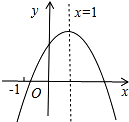 ��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����н��ۣ�
��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����н��ۣ�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com