
(2014•莱芜)如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,下列说法不正确的是( )

A.△CDF的周长等于AD+CD
B.FC平分∠BFD
C.AC2+BF2=4CD2
D.DE2=EF•CE
B
【解析】
试题分析:首先由正五边形的性质可得AB=BC=CD=DE=AE,BA∥CE,AD∥BC,AC∥DE,AC=AD=CE,根据有一组邻边相等的平行四边形是菱形即可证得四边形ABCF为菱形,得CF=AF,即△CDF的周长等于AD+CD,由菱形的性质和勾股定理得出AC2+BF2=4CD2,可证明△CDE∽△DFE,即可得出DE2=EF•CE.
【解析】
∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=AE,BA∥CE,AD∥BC,AC∥DE,AC=AD=CE,
∴四边形ABCF是菱形,
∴CF=AF,
∴△CDF的周长等于CF+DF+CD,
即△CDF的周长等于AD+CD,
故A选项正确;
∵四边形ABCF是菱形,
∴AC⊥BF,
设AC与BF交于点O,
由勾股定理得OB2+OC2=BC2,
∴AC2+BF2=(2OC)2+(2OB)2=4OC2+4OB2=4BC2,
∴AC2+BF2=4CD2.
故C选项正确;
由正五边形的性质得,△ADE≌△CDE,
∴∠DCE=∠EDF,
∴△CDE∽△DFE,
∴ =
= ,
,
∴DE2=EF•CE,
故D选项正确;
故选:B.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:[同步]2014年人教版初中数学七年级上第四章4.4练习卷(解析版) 题型:选择题
(2013•菏泽)如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120° 的菱形,剪口与第二次折痕所成角的度数应为( )

A.15°或30° B.30°或45° C.45°或60° D.30°或60°
查看答案和解析>>
科目:初中数学 来源:[同步]2014年人教版初中数学九年级上第二十三章23.3练习卷(解析版) 题型:
(2014•普陀区一模)用放大镜将图形放大,应该属于( )
A.平移变换 B.相似变换 C.对称变换 D.旋转变换
查看答案和解析>>
科目:初中数学 来源:[同步]2014年人教版初中数学九年级上第二十三章24.3练习卷(解析版) 题型:选择题
(2014•闵行区三模)如图,在⊙O中,OA=AB,OC⊥AB,交⊙O于点C,那么下列结论错误的是( )

A.∠BAC=30°
B.弧AC等于弧BC
C.线段OB的长等于圆内接正六边形的半径
D.弦AC的长等于圆内接正十二边形的边长
查看答案和解析>>
科目:初中数学 来源:[同步]2014年人教版初中数学九年级上第二十三章24.3练习卷(解析版) 题型:选择题
(2014•安徽模拟)如图,把正△ABC的外接圆对折,使点A与劣弧 的中点M重合,折痕分别交AB、AC于D、E,若BC=5,则线段DE的长为( )
的中点M重合,折痕分别交AB、AC于D、E,若BC=5,则线段DE的长为( )

A. B.
B. C.
C. D.
D.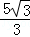
查看答案和解析>>
科目:初中数学 来源:[同步]2014年人教版初中数学九年级上第二十三章23.3练习卷(解析版) 题型:
(2013•静安区二模)一个图形沿一条直线翻折后再沿这条直线的方向平移,我们把这样的图形运动称为图形的翻移,这条直线称为翻移线.如图△A2B2C2是由△ABC沿直线l翻移后得到的.在下列结论中,图形的翻移所具有的性质是( )

A.各对应点之间的距离相等 B.各对应点的连线互相平行
C.对应点连线被翻移线平分 D.对应点连线与翻移线垂直
查看答案和解析>>
科目:初中数学 来源:[同步]2014年人教版初中数学九年级上第二十三章23.3练习卷(解析版) 题型:
(2013•长沙)在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:[同步]2014年人教版初中数学九年级下第二十九章29.1练习卷(解析版) 题型:选择题
(2011•天河区一模)下面四幅图是在同一天同一地点不同时刻太阳照射同一根旗杆的影像图,其中表示太阳刚升起时的影像图是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源:[同步]2014年北师大版初中数学七年级上第一章1.3练习卷(解析版) 题型:选择题
(2013•沙市区三模)如图是一个底面为正方形的长方形,现将左图中的长方体切掉一个“角”后变成了右图的几何体,则右图的俯视图是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com