练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图①两条直线交于一点，图中共有
    (4-2)×4
    4
    =2    对对顶角；如图②三条直线交于一点，图中共有
    (6-2)×6
    4
    =6    对对顶角；如图③四条直线交于一点，图中共有
    (8-2)×8
    4
    =12    对对顶角；…；按这样的规律，六条直线交于一点，那么图中共有
    (12-2)×12
    4
    =30
    (12-2)×12
    4
    =30
    对对顶角；若n条直线交于一点，则共有
    n2-n
    n2-n
    对对顶角．（用含n的式子表示）
    分析：根据提供的规律，对顶角的对数等于直线条数的2倍乘以2倍减2，然后除以4，进行计算即可得解．
    解答：解：根据规律，六条直线交于一点，共有
    (12-2)×12
    4
    =30对对顶角；
    n条直线交于一点，共有
    (2n-2)•2n
    4
    =n2-n对对顶角．
    故答案为：
    (12-2)×12
    4
    =30；n2-n．
    点评：本题考查了对顶角的对数的变化规律，读懂题目信息，理解对顶角对数的求解方法是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2013•株洲）已知抛物线C1的顶点为P（1，0），且过点（0，
    1
    4
    ）．将抛物线C1向下平移h个单位（h＞0）得到抛物线C2．一条平行于x轴的直线与两条抛物线交于A、B、C、D四点（如图），且点A、C关于y轴对称，直线AB与x轴的距离是m2（m＞0）．
    （1）求抛物线C1的解析式的一般形式；
    （2）当m=2时，求h的值；
    （3）若抛物线C1的对称轴与直线AB交于点E，与抛物线C2交于点F．求证：tan∠EDF-tan∠ECP=
    1
    2
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知抛物线C1的顶点为P（1，0），且过点（0，数学公式）．将抛物线C1向下平移h个单位（h＞0）得到抛物线C2．一条平行于x轴的直线与两条抛物线交于A、B、C、D四点（如图），且点A、C关于y轴对称，直线AB与x轴的距离是m2（m＞0）．
    （1）求抛物线C1的解析式的一般形式；
    （2）当m=2时，求h的值；
    （3）若抛物线C1的对称轴与直线AB交于点E，与抛物线C2交于点F．求证：tan∠EDF-tan∠ECP=数学公式．

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（湖南株洲卷）数学（解析版） 题型：解答题

    已知抛物线C1的顶点为P（1，0），且过点（0，）．将抛物线C1向下平移h个单位（h＞0）得到抛物线C2．一条平行于x轴的直线与两条抛物线交于A、B、C、D四点（如图），且点A、C关于y轴对称，直线AB与x轴的距离是m2（m＞0）．

    （1）求抛物线C1的解析式的一般形式；

    （2）当m=2时，求h的值；

    （3）若抛物线C1的对称轴与直线AB交于点E，与抛物线C2交于点F．求证：tan∠EDF﹣tan∠ECP=．

     

    查看答案和解析>>

    科目：初中数学 来源：2014届福建福清市七年级下学期期中模拟数学卷（解析版） 题型：填空题

    如图①两条直线交于一点，图中共有对对顶角；如图②三条直线交于一

    点，图中共有对对顶角；如图③四条直线交于一点，图中共有

    对对顶角；…；按这样的规律，六条直线交于一点，那么图中共有           对对顶角；

    若n条直线交于一点，则共有           对对顶角.（用含n的式子表示）

                                                             

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

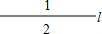    作业宝（1）一条直线可以把平面分成两个部分（或区域），如图，两条直线可以把平面分成几个部分？三条直线可以把平面分成几个部分？试画图说明．
    （2）四条直线最多可以把平面分成几个部分？试画出示意图，并说明这四条直线的位置关系．
    （3）平面上有n条直线．每两条直线都恰好相交，且没有三条直线交于一点，处于这种位置的n条直线分一个平面所成的区域最多，记为an，试研究an与n之间的关系．

    查看答案和解析>>

    同步练习册答案