
【题目】如图,直线y=x+4与双曲线y= ![]() (k≠0)相交于A(﹣1,a)、B两点,在y轴上找一点P,当PA+PB的值最小时,点P的坐标为 .
(k≠0)相交于A(﹣1,a)、B两点,在y轴上找一点P,当PA+PB的值最小时,点P的坐标为 . 
【答案】(0, ![]() )
)
【解析】解:把点A坐标代入y=x+4得, ﹣1+4=a,
a=3,
即A(﹣1,3),
把点A坐标代入双曲线的解析式:3=﹣k,
解得:k=﹣3,
联立两函数解析式得: 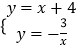 ,
,
解得: ![]() ,
, ![]() ,
,
即点B坐标为:(﹣3,1),
作出点A关于y轴的对称点C,连接BC,与y轴的交点即为点P,使得PA+PB的值最小,
则点C坐标为:(1,3),
设直线BC的解析式为:y=ax+b,
把B、C的坐标代入得: ![]() ,
,
解得: ![]() ,
,
函数解析式为:y= ![]() x+
x+ ![]() ,
,
则与y轴的交点为:(0, ![]() ).
).
所以答案是:(0, ![]() ).
).
【考点精析】认真审题,首先需要了解轴对称-最短路线问题(已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径).


科目:初中数学 来源: 题型:
【题目】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下: 如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.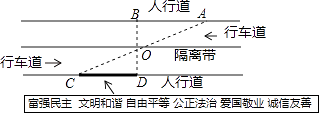
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的两格中,点A、B、C都是格点.
(1)将△ABC向左平移6个单位长度得到得到△A1B1C1;
(2)将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2 , 请画出△A2B2C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=2x+2的图象与x轴交于A,与y轴交于点C,点B的坐标为(a,0),(其中a>0),直线l过动点M(0,m)(0<m<2),且与x轴平行,并与直线AC、BC分别相交于点D、E,P点在y轴上(P点异于C点)满足PE=CE,直线PD与x轴交于点Q,连接PA.
(1)写出A、C两点的坐标;
(2)当0<m<1时,若△PAQ是以P为顶点的倍边三角形(注:若△HNK满足HN=2HK,则称△HNK为以H为顶点的倍边三角形),求出m的值;
(3)当1<m<2时,是否存在实数m,使CDAQ=PQDE?若能,求出m的值(用含a的代数式表示);若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ= ![]() ,那么当点P运动一周时,点Q运动的总路程为 .
,那么当点P运动一周时,点Q运动的总路程为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com