
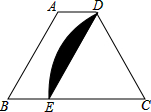
 如图,四边形ABED是平行四边形,B、E、C三点共线,以点C为圆心,CDWie半径的弧与BC交于点E,AB=CD=4,则阴影部分的面积是$\frac{8}{3}$π-4$\sqrt{3}$.
如图,四边形ABED是平行四边形,B、E、C三点共线,以点C为圆心,CDWie半径的弧与BC交于点E,AB=CD=4,则阴影部分的面积是$\frac{8}{3}$π-4$\sqrt{3}$. 分析 根据平行四边形的性质得出DE=4,求出△CDE是等边三角形,求出等边△CDE的面积和扇形DCE的面积,即可得出答案.
解答 解:过D作DF⊥EC于F,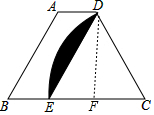
∵四边形ABED是平行四边形,AB=4,
∴DE=AB=4,
∵CE=CD=4,
∴△CED是等边三角形,
∴∠C=60°,
∵∠DFC=90°,
∴∠CDF=30°
∴CF=$\frac{1}{2}$CD=2,由勾股定理得:DF=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴等边三角形CDE的面积为$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$,
扇形ECD的面积为$\frac{60π×{4}^{2}}{360}$=$\frac{8}{3}$π,
即阴影部分的面积S=$\frac{8}{3}$π-4$\sqrt{3}$,
故答案为:$\frac{8}{3}$π-4$\sqrt{3}$.
点评 本题考查了平行四边形的性质,扇形的面积计算等知识点,能求出△CDE的面积和扇形ECD的面积是解此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
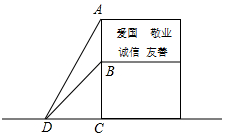 为了弘扬“社会主义核心价值观”,区政府在广场上竖立了如图所示的公益广告牌,并在两侧加固钢缆,已知钢缆底端D到达广告牌立柱AC的距离为5米,从点D测得广告牌顶端A点和底端B点的仰角分别为60°和45°,求广告牌的高度AB.
为了弘扬“社会主义核心价值观”,区政府在广场上竖立了如图所示的公益广告牌,并在两侧加固钢缆,已知钢缆底端D到达广告牌立柱AC的距离为5米,从点D测得广告牌顶端A点和底端B点的仰角分别为60°和45°,求广告牌的高度AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )
在平面直角坐标系中,O为原点,点A(-3,0),点B(0,3),点E、点F分别为OA,OB的中点,若正方形OEDF绕点O顺时针旋转,得到正方形OE′D′F′,若直线AE′与直线BF′相交于点P,则点P的纵坐标的最大值是( )| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\frac{\sqrt{3}+3}{2}$ | C. | $\frac{\sqrt{3}+3}{4}$ | D. | $\frac{3\sqrt{3}+3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com