
�ס�������֮����һ����ֱ�Ĺ�·L��С���Ӽس����ع�·L����ǰ���ҵأ�ͬʱС�����ҵس����ع�·L�����г�ǰ���أ�С�������ͣ��һ��ʱ�䣬��ԭ·ԭ�ٷ��أ���С��������һ���е��ҵأ���ͼ���߶�OA��ʾС����صľ���Ϊy1�����������ߵ�ʱ��Ϊx�����ӣ�֮��ĺ�����ϵ������BCDEA��ʾС����صľ���Ϊy2�����������ߵ�ʱ��Ϊx�����ӣ�֮��ĺ�����ϵ.�����ͼ�����������⣺
��1��С�����е��ٶ��� ��/���ӣ�С�������г����ٶ� ��/���ӣ�
��2��ͼ�е�F�����ǣ� �� ������E�����ǣ� �� ����
��3����y1��y2��x֮��ĺ�����ϵʽ��
��4����ֱ��д��С�����ҵ������ٻص��ҵع����У�������������С�����300�ף�
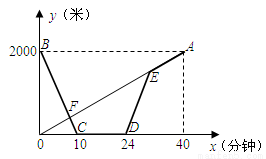
(1)50��200����2��8��400��32��1600����3��y1=50x��y2=��200x+2000����4������6.8���ӣ�9.2���ӣ�25.5����ʱ��С�����300�ף�
��������
�����������1������ͼ���֪С�����е��ٶ���2000��40=50��/���ӣ�С�������г����ٶ�2000��10=200��/���ӣ�
��2����3���ֱ���С����С����صľ���Ϊy1���ף���y2���ף���x�����ӣ�֮��ĺ�����ϵʽΪy1=k1x��y2=k2x+b���ɴ���ϵ��������ͼ��Ϳ����������ʽ���ٽ�һ����ý�������꣬�ó���F��E�����꼴�ɣ�
��4�����������������Ĺ�����С����С�����300��̽�ֵó��𰸼��ɣ�
�����������1��С�����е��ٶ���2000��40=50��/���ӣ�С�������г����ٶ�2000��10=200��/���ӣ�
��2����С����صľ���Ϊy1���ף���x�����ӣ�֮��ĺ�����ϵʽΪy1=k1x��
����㣨40��2000���ã�2000=40k1�����k1=50��
����y1=50x��
��С����صľ���Ϊy2���ף���x�����ӣ�֮��ĺ�����ϵʽΪy2=k2x+b��
�����㣨0��2000���ͣ�10��0����
 ��
��
����yBC=��200x+2000��
��ͼ��֪24����ʱ���˵ľ���Ϊ��S=24��50=1200��
С���Ӽ���С����ʱ��Ϊ24��50�£�200��50��=8���ӣ�
Ҳ����32����ʱΪ0����y1=50x=1600�����E����Ϊ��32��1600����
�������
 ��
��
���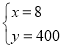 ��
��
����ͼ�е�F�����ǣ�8��400����
��3���ɣ�2����֪y1=50x��
yBC=��200x+2000��0��x��10����
��S��x֮��ĺ�����ϵʽΪ��S=kx+b�������⣬
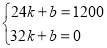 ��
��
��ã�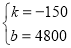 ��
��
��S=��150x+4800��
��yED=��150x+4800��24��x��32����
��4����0��x��10ʱ��
��2000��300���£�50+200��=6.8�����ӣ�
��8��x��10��
300�£�50+200��+8=9.2�����ӣ�
��24��x��32��
��50x������150x+4800��=300��
���x=25.5�����ӣ�
��С�����ҵس����ٻص��ҵع����У�����6.8���ӣ�9.2���ӣ�25.5����ʱ��С�����300�ף�
���㣺һ�κ�����Ӧ�ã�


 �żӾ���ϵ�д�
�żӾ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡʯ��ׯ�����ذ��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�������
��1��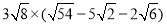
��2��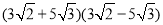
��3��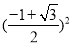
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡʯ��ׯ�а��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
��ƽ��ֱ������ϵ�У���M����2��3���ڣ�������
A����һ���� B���ڶ����� C���������� D����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡ�����ذ��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
һ���ִ���ͬһ�����������ڼס�����������֪�ִ��ھ�ˮ�е��ٶ�Ϊ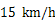 ��ˮ�� �ٶ�Ϊ
��ˮ�� �ٶ�Ϊ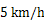 ���ִ��ȴӼ�˳ˮ���е��ҵأ����ҵ�ͣ��һ��ʱ����ִ��ҵ���ˮ���з��ص��������ִ��Ӽس���������ʱ��Ϊ
���ִ��ȴӼ�˳ˮ���е��ҵأ����ҵ�ͣ��һ��ʱ����ִ��ҵ���ˮ���з��ص��������ִ��Ӽس���������ʱ��Ϊ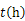 �����е�·��Ϊ
�����е�·��Ϊ 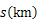 ����
����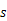 ��
��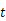 �ĺ���ͼ������� �� ��
�ĺ���ͼ������� �� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡ�����ذ��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
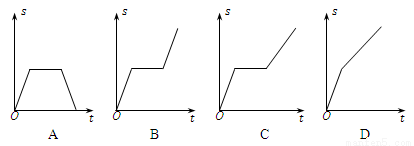
��֪��P��a+1,2a��3������x��ĶԳƵ��ڵ�һ���ޣ���a��ȡֵ��Χ�ǣ� ��
A��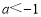 B��
B��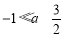
C��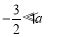 D��
D��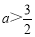
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡ��ɽ�а��꼶��ѧ����ĩ����ѧ�Ծ��������棩 ���ͣ������
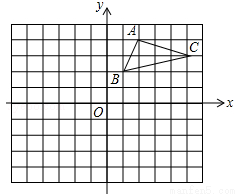
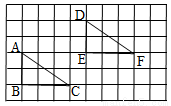
��ͼ����ƽ��ֱ������ϵ�У���ABC���������㶼�ڸ���ϣ���A������Ϊ��2��4���������������⣺
��1��������ABC����x��ԳƵ���A1B1C1����д����C1�������� �� ����
��2������ABC�����������ĺᡢ�����궼���ԣ�1���ֱ�õ���Ӧ��A2��B2��C2��������A2B2C2������ABC����A2B2C2���� �Գƣ�
��3������ABC��������ƽ�ƣ�ʹ��B�Ķ�Ӧ��B3����Ϊ����6��1����������A3B3C3.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015��ӱ�ʡ��ɽ�а��꼶��ѧ����ĩ����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ����֪����ABCD ��һ��ֱ�߽��þ��� ABCD �ָ����������Σ�������������ε��ڽǺͷֱ�Ϊ M�� N����M �� N ���������� ��
A ��360�� B ��540�� C��720�� D ��630��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�߰��а��꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ������
ij��˾��ƸְԱ���Լס�����λ��ѡ�˽��������Ժͱ��ԣ������а�������Ϳڲţ������а���רҵˮƽ�ʹ����������죬���ǵijɼ����ٷ��ƣ����±���
��ѡ�� | ���� | ���� | ||
���� | �ڲ� | רҵˮƽ | �������� | |
�� | 86 | 90 | 96 | 92 |
�� | 92 | 88 | 95 | 93 |
��1������˾���ݾ�Ӫ���ʺ�λҪ����Ϊ�����塢�ڲš�רҵˮƽ��������������5��5��4��6�ı�ȷ���������ס������˸��Ե�ƽ���ɼ�������˭����¼ȡ��
��2������˾���ݾ�Ӫ���ʺ�λҪ����Ϊ�����Գɼ�������ռ5%���ڲ�ռ30%�����Գɼ���רҵˮƽռ35%����������ռ30%����ô����Ϊ�ù�˾Ӧ��¼ȡ˭��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ���꼶��ѧ����ѧ������ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ�� ����������ƽ�Ƶõ�
����������ƽ�Ƶõ�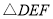 ( )
( )
A���� ����ƽ��4����λ��������ƽ��2����λ
����ƽ��4����λ��������ƽ��2����λ
B���� ����ƽ��4����λ��������ƽ��2����λ
����ƽ��4����λ��������ƽ��2����λ
C����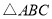 ����ƽ��4����λ��������ƽ��2����λ
����ƽ��4����λ��������ƽ��2����λ
D����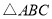 ����ƽ��4����λ��������ƽ��2����λ
����ƽ��4����λ��������ƽ��2����λ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com