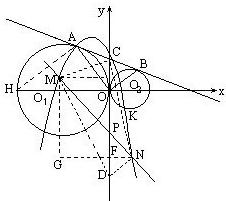
解:(1)如图,
连接HA,BK.
∵AB、OC是两圆的公切线,
∴OC=AC=BC;
∴∠AOB=90°,
∴AB=

=6
∴OC=3
∴C(0,3);
∵HO是⊙O
1的直径,
∴∠HAO=∠AOB=90°;
∵AB是⊙O
1的切线,
∴∠BAO=∠OHA,
∴△AOH∽△OBA,
∴

∴
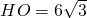
∴
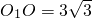
∴O1的坐标是(-3

,0)
设经过O
1、C、O
2三点的抛物线的解析式为y=ax
2+bx+c;
∴由c=3,0=27a-3
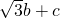
,0=3a+

b+c
可得a=-

,b=-

,c=3
∴
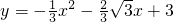
;
(2)设直线y=kx+m与y轴交于点P(0,m),交抛物线于点M(x
1,y
1)、N(x
2,y
2).
分别由M、N向y轴引垂线,垂足为E、F;
∵MP=NP,∠MPE=∠NPF,∠MEP=∠NFP=90°,
∴△MPE≌△NPF,
∴ME=NF,即|x
1|=|x
2|;
又∵M、N在y轴两侧,
∴x
1、x
2异号,
∴x
1+x
2=0;
设
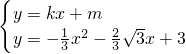
消去y并整理,得x
2+(3k+2

)x+3(m-3)=0
∴
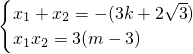
∵x
1+x
2=0
∴
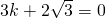
∴

(3)过M作NF的垂线,交NF的延长线于G.
则NG=|x
1-x
2|=
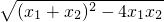
=
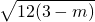
MG=|y
1-y
2|=|k(x
1-x
2)|=

=
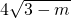
∴MN
2=NC2+MG
2=28(3-m),
∴

∵四边形MDNC是矩形,
∴

又∵PC=|3-m|,
∴

∴m
2+m-12=0,
∴m=-4或m=3(舍去,
∵点D在y轴负半轴上);
∴PC=7,
∴PD=7;
∴OD=OP+PD=11,
∴D(0,-11);
即当点D的坐标为(0,-11)时,四边形MDNC为矩形.
分析:(1)由于CO、AB都是两圆的切线,根据切线长定理可求得OC=AC=BC,即可得到∠AOB=90°,在Rt△AOB中,根据勾股定理可求出AB的长,进而可得到OC的值,即C点的坐标;连接HA,证△HAO∽△AOB,通过相似三角形得到的比例线段即可求出OH的长,由此可求得O
1的坐标,同理可求出O
2的坐标,进而可用待定系数求出抛物线的解析式;
(2)过M、N分别作y轴的垂线,设垂足为E、F,若MN被y轴平分,那么MP=PN,可证得△MPE≌△NPF,由此得到M、N的横坐标互为相反数,即两者的和为0;可联立直线与抛物线的解析式,可得到关于x的一元二次方程,那么M、N两点的横坐标即为方程的两个根,已求得两根的和为0,可根据韦达定理求出k的值;
(3)根据M、N的坐标可求出MN的长,若四边形MDNC是矩形,那么对角线MN、CD相等且互相平分,则PC=12MN,由此可求出待定系数m的值,进而可求出PC、PD的长,也就能得到D点的坐标.
点评:此题主要考查了相切两圆的性质,切线长定理,直角三角形、相似三角形、全等三角形的判定和性质,以及矩形的判定等,综合性强,难度较大.

 ,OB=3.
,OB=3. DNC是矩形?
DNC是矩形? 解:(1)如图,
解:(1)如图, =6
=6
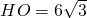
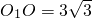
 ,0)
,0)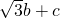 ,0=3a+
,0=3a+ b+c
b+c ,b=-
,b=- ,c=3
,c=3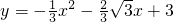 ;
;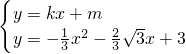
 )x+3(m-3)=0
)x+3(m-3)=0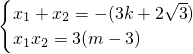
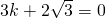

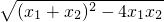 =
=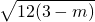
 =
=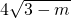





 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案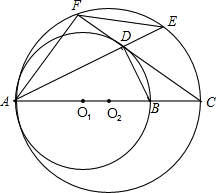 O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.
O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.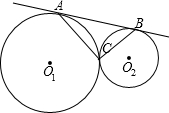 已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=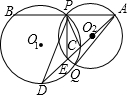 (1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且
(1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且