
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=DC,点E在对角线BD上,作∠ECF=90°,连接DF,且满足CF=EC.
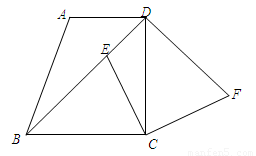
(1)求证:BD⊥DF;
(2)当 时,试判断四边形DECF的形状,并说明理由.
时,试判断四边形DECF的形状,并说明理由.
(1)由 可得
可得 ,再结合
,再结合 即可证得
即可证得 ≌
≌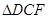 ,则
,则 ,由
,由 可得
可得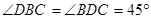 ,即可得到
,即可得到 ,从而可以证得结论;
,从而可以证得结论;
(2)由 ,可得
,可得 ,再结合
,再结合 可证得
可证得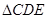 ∽
∽ ,即可得到
,即可得到 ,再结合
,再结合 可得四边形
可得四边形 是矩形,从而可以作出判断.
是矩形,从而可以作出判断.
【解析】
试题分析:(1)由 可得
可得 ,再结合
,再结合 即可证得
即可证得 ≌
≌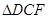 ,则
,则 ,由
,由 可得
可得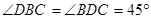 ,即可得到
,即可得到 ,从而可以证得结论;(2)正方形
,从而可以证得结论;(2)正方形
(1)∵ ,
,
∴
∵ ,
,
∴ ≌
≌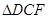
∴
∵ ,
,
∴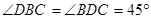
∴ ,
,
∴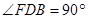
∴ ;
;
(2)四边形 是正方形
是正方形
∵ ,
,
∴ ,
,
∴
∵ ∴
∴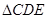 ∽
∽
∴
∵ ,
,
∴四边形 是矩形
是矩形
∵ ,
,
∴四边形 是正方形.
是正方形.
考点:全等三角形的判定和性质,相似三角形的判定和性质,矩形、正方形的判定
点评:全等三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com