
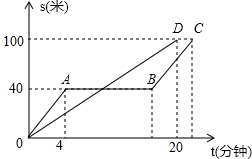
 同学们都非常熟悉“龟兔赛跑”的故事,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
同学们都非常熟悉“龟兔赛跑”的故事,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.分析 (1)利用乌龟始终运动,中间没有停留,进而得出线段OD的意义和全程的距离;
(2)根据图象求出乌龟的速度;
(3)利用兔子睡觉前行驶的路程是40米,结合乌龟的速度求出所用的时间;
(4)利用兔子的速度,求出兔子走完全程的时间,再求解即可.
解答 解:(1)由题意可得:线段OD表示赛跑过程中乌龟的路程与时间的关系,
赛跑的全程是:100m;
故答案为:乌龟,100;
(2)乌龟每分钟爬:100÷20=5(米/分钟);
故答案为:5;
(3)如图所示:乌龟爬行40米时追上兔子,此时用时:40÷5=8(分钟);
故答案为:8;
(4)∵兔子跑了40米停下睡觉,用了4分钟,
∴剩余60米,所用的时间为:60÷12=5(分钟),
∴兔子睡觉用了:22-4-5=13(分钟).
故答案为:13.
点评 本题考查了函数图象,理解两个函数图象的交点表示的意义,从函数图象准确获取信息是解题的关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
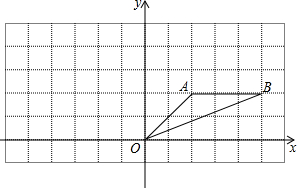 如图在平面直角坐标系中,已知点A(2,2),B(5,2).
如图在平面直角坐标系中,已知点A(2,2),B(5,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
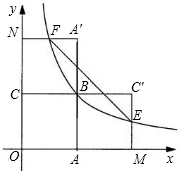 如图,四边形OABC是面积为4的正方形,双曲线经过点B.
如图,四边形OABC是面积为4的正方形,双曲线经过点B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com