
分析 (1)将原方程分解为(x-3)(x-1)=0,然后解得方程两个根即可;
(2)将原方程去分母得2x+2=x-2,然后解得这个一元一次方程,最后检验方程的根即可.
解答 解:(1)∵x2-4x+3=0,
∴(x-3)(x-1)=0,
∴x-3=0或x-1=0,
∴x1=3,x2=1;
(2)∵$\frac{2x}{x-2}$-$\frac{2}{2-x}$=1,
∴$\frac{2x}{x-2}$+$\frac{2}{x-2}$=1,
∴2x+2=x-2,
∴x=-4,
经检验,-4-2≠0,2-(-4)≠0,
所以x=-4是原方程的解.
点评 本题主要考查了熟练掌握并运用因式分解法解一元二次方程的一般步骤:①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.还考查了(1)解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.(2)解分式方程时,去分母后所得整式方程的解有可能使原方程中的分母为0,所以应如下检验:①将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解.②将整式方程的解代入最简公分母,如果最简公分母的值为0,则整式方程的解不是原分式方程的解.所以解分式方程时,一定要检验.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
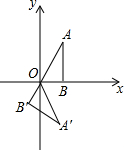 如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O按顺时针方向旋转120°得到△OA′B′,则点A′的坐标是(2,-2$\sqrt{3}$).
如图,点B在x轴上,∠ABO=90°,∠A=30°,OA=4,将△OAB绕点O按顺时针方向旋转120°得到△OA′B′,则点A′的坐标是(2,-2$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>n | B. | m<n | C. | m=n | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{7}{2}$ | B. | -$\frac{1}{2}$ | C. | -2 | D. | -$\frac{9}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了了解全国中学生的视力情况,选择全面调查 | |
| B. | 为了了解一批袋装食品是否含有防腐剂,选择全面调查 | |
| C. | 为了检测某城市的空气质量,选择抽样调查 | |
| D. | 为了检测乘坐飞机的旅客是否携带违禁物品,选择抽样调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$(k>0)的图象与BC边交于点E.
如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$(k>0)的图象与BC边交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
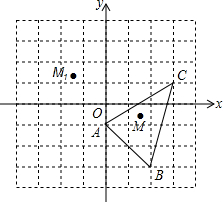 如图,在平面直角坐标中,三角形ABC中任意一点M(x,y)平移后的对应点为M1(x-3,y+2),已知:A(0,-1),B(2,-3),C(3,1).
如图,在平面直角坐标中,三角形ABC中任意一点M(x,y)平移后的对应点为M1(x-3,y+2),已知:A(0,-1),B(2,-3),C(3,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com