Question

6．设O为锐角△ABC的外心，R为△ABC的外接圆半径，AO，BO，CO的延长线分别交BC，CA，AB于点D，E，F．求证：$\frac{1}{AD}$+$\frac{1}{BE}$+$\frac{1}{CF}$=$\frac{2}{R}$．

Answer 1

分析 延长AD交⊙O于M，由于AD，BE，CF共点O．根据S_△ABC=S_△ABO+S_△ACO+S_△BCO、$\frac{OD}{AD}=\frac{{S}_{△OBC}}{{S}_{△ABC}}$，$\frac{OE}{BE}$=$\frac{{S}_{△OAC}}{{S}_{△BAC}}$，$\frac{OF}{CF}$=$\frac{{S}_{△OAB}}{{S}_{△CAB}}$，可以推知$\frac{OD}{AD}+\frac{OE}{BE}+\frac{OF}{CF}=1$①；然后由OD=R-DM、AM=2R求得=$\frac{R-DM}{2R-DM}$=1-$\frac{R}{AD}$、$\frac{OE}{BE}=1-\frac{R}{BE}$，$\frac{OF}{CF}$=1-$\frac{R}{CF}$；最后将其代入①式求得结论．

解答 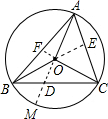证明：延长AD交⊙O于M，由于AD，BE，CF共点O，
∴$\frac{OD}{AD}=\frac{{S}_{△OBC}}{{S}_{△ABC}}$，$\frac{OE}{BE}$=$\frac{{S}_{△OAC}}{{S}_{△BAC}}$，$\frac{OF}{CF}$=$\frac{{S}_{△OAB}}{{S}_{△CAB}}$，
则$\frac{OD}{AD}+\frac{OE}{BE}+\frac{OF}{CF}=1$…①；
而$\frac{OD}{AD}$=$\frac{R-DM}{2R-DM}$=1-$\frac{R}{2R-DM}$=1-$\frac{R}{AD}$，
同理有，$\frac{OE}{BE}=1-\frac{R}{BE}$，$\frac{OF}{CF}$=1-$\frac{R}{CF}$，
代入①得：（1-$\frac{R}{AD}$）+（1-$\frac{R}{BE}$）+（1-$\frac{R}{CF}$）=1…②，
∴$\frac{R}{AD}$+$\frac{R}{BE}$+$\frac{R}{CF}$=2，
∴$\frac{1}{AD}$+$\frac{1}{BE}$+$\frac{1}{CF}$=$\frac{2}{R}$．

点评 本题考查了面积以及等积变换．解答本题时，通过作辅助线AM，将AD、OD、CO、CF、BO、BE的长度与半径R联系在一起，从而通过化$\frac{OD}{AD}+\frac{OE}{BE}+\frac{OF}{CF}=1$，证得结$\frac{1}{AD}$+$\frac{1}{BE}$+$\frac{1}{CF}$=$\frac{2}{R}$．