
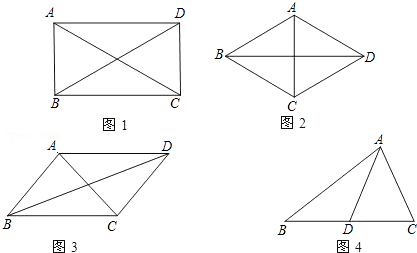
���� ��1���������εĶԽ�����ƽ���Ҵ�ֱ�Լ����ɶ�������֤�����ɣ�
��2����AE��BC�ڵ�E��DF��BC��BC���ӳ�����F��֤��AE=DF��BE=CF�����ݾ��ε�����֤�����ɣ�
��3���ӳ�AD��E��ʹDE=AD������BE��CE������ƽ���ı��Σ��ɣ�2���Ľ��۴�����ֵ���ɣ�
��� �⣺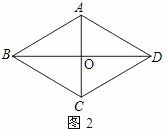 ��1����ͼ2����AC��BD�ཻ�ڵ�O��
��1����ͼ2����AC��BD�ཻ�ڵ�O��
���ı���ABCD�����Σ�
��AC��BD��AC=2OA��BD=2OB��
��Rt��AOB�У��ɹ��ɶ�������
OA2+OB2=AB2��
��AC2+BD2=4OA2+4OB2=4��OA2+OB2��=4AB2��
�֡�AB=BC��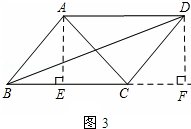
��AC2+BD2=2��AB2+AB2��=2��AB2+BC2����
��2�����IJ��������
֤������ͼ��3����AE��BC�ڵ�E��DF��BC��BC���ӳ�����F��
���AEB=��DFC=90�㣮
���ı���ABCD��ƽ���ı��Σ�
��AB=DC��AB��CD��
���ABE=��DCF��
���ABE�ա�DCF��
��AE=DF��BE=CF��
��Rt��ACE��Rt��BDF�У��ɹ��ɶ����ã�
AC2=AE2+EC2=AE2+��BC-BE��2��
BD2=DF2+BF2=DF2+��BC+CF��2=AE2+��BC+BE��2��
��AC2+BD2=2AE2+2BC2+2BE2=2��AE2+BE2��+2BC2��
�֡�AE2+BE2=AB2��
��AC2+BD2=2��AB2+BC2����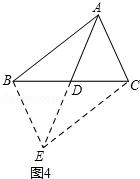 ��3����ͼ4���ӳ�AD��E��ʹDE=AD������BE��CE����AE=2AD��
��3����ͼ4���ӳ�AD��E��ʹDE=AD������BE��CE����AE=2AD��
��BD=CD��
���ı���ABEC��ƽ���ı��Σ�
�ɣ�2���Ľ��ۣ���
AE2+BC2=2��AB2+AC2����
����2AD��2+a2=2��b2+c2����
���AD2=$\frac{1}{4}$��2b2+2c2-a2����
��AD=$\frac{1}{2}$$\sqrt{2{b}^{2}+2{c}^{2}-{a}^{2}}$��
���� ���⿼����Ǿ��Ρ����κ�ƽ���ı��ε������Լ����ɶ�����Ӧ�ã���������ƽ���ı��ε����ʶ������ɶ����ǽ���Ĺؼ���ע�������ε����ߵ����ʵ�������ã�


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
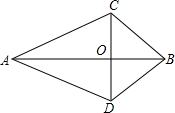 ��ͼ��AC=AD��BC=BD�������н����ȷ���ǣ�������
��ͼ��AC=AD��BC=BD�������н����ȷ���ǣ�������| A�� | ��ABC=��CAB | B�� | OA=OB | C�� | ��ACD=��BDC | D�� | AB��CD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=-1��y=1 | B�� | x=1��y=-1 | C�� | x=-1��y=-1 | D�� | x=1��y=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
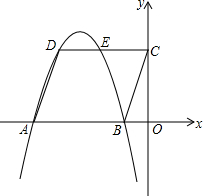 ��֪��ƽ���ı���ABCD��ֱ������ϵ�е�λ����ͼ��O������ԭ�㣬OB��OC��OA=1��3��5��S��ABCD=12�������߾���D��A��B���㣮
��֪��ƽ���ı���ABCD��ֱ������ϵ�е�λ����ͼ��O������ԭ�㣬OB��OC��OA=1��3��5��S��ABCD=12�������߾���D��A��B���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
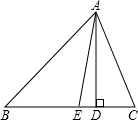 ��ͼ����֪��ABC�У�AD��BC���ϵĸߣ���E���߶�BD�ϣ���AEƽ�֡�BAC������B=40�㣬��C=78�㣬���EAD=19�㣮
��ͼ����֪��ABC�У�AD��BC���ϵĸߣ���E���߶�BD�ϣ���AEƽ�֡�BAC������B=40�㣬��C=78�㣬���EAD=19�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
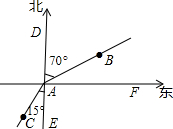 ��ͼ���״�A�������ƫ��70�㷽����50m����B���Ҵ�A���������ƫ��15�㷽����60m����C�����BAC�Ķ����ǣ�������
��ͼ���״�A�������ƫ��70�㷽����50m����B���Ҵ�A���������ƫ��15�㷽����60m����C�����BAC�Ķ����ǣ�������| A�� | 85�� | B�� | 160�� | C�� | 125�� | D�� | 105�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com