
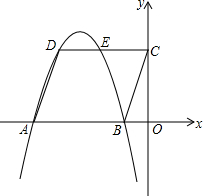
 已知:平行四边形ABCD在直角坐标系中的位置如图,O是坐标原点,OB:OC:OA=1:3:5,S□ABCD=12,抛物线经过D、A、B三点.
已知:平行四边形ABCD在直角坐标系中的位置如图,O是坐标原点,OB:OC:OA=1:3:5,S□ABCD=12,抛物线经过D、A、B三点.分析 (1)由OB:OC:OA=1:3:5,S?ABCD=12,求得OB=1,OC=3,OA=5,进而求得A、C两点的坐标;
(2)由OB=1,OC=3,OA=5,得出AB=4,根据平行四边形等边平行且相等,得出D(-4,3),然后根据待定系数法即可求得抛物线解析式;
(3)先求得E的坐标,进而求得DE的长,根据以DE为边的平行四边形的面积与?ABCD面积相等,求得P点到直线DE的距离为6,从而求得P的纵坐标为-3,代入抛物线的解析式即可求得P的坐标.
解答 解:(1)∵OB:OC:OA=1:3:5,
设OB=x,OC=3x,OA=5x,
∴AB=OA-OB=5x-x=4x,
∵S?ABCD=12,
∴AB•OC=4x×3x=12,解得x=1,
∴OB=1,OC=3,OA=5,
∴A(-5,0),C(0,3),
(2)∵OB=1,OC=3,OA=5,
∴AB=4,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∴D(-4,3),
∵A(-5,0),B(-1,0),
设抛物线的解析式为y=ax2+bx+c,
∴$\left\{\begin{array}{l}16a-4b+c=3\\ 25a-5b+c=0\\ a-b+c=0\end{array}\right.$,解得$\left\{\begin{array}{l}a=-1\\ b=-6\\ c=-5\end{array}\right.$,
∴抛物线的解析式为y=-x2-6x-5.
(3)∵E点的纵坐标为3,
∴-x2-6x-5=3.解得x=-2或x=-4,
∴E的坐标为(-2,3),
∴DE=-2-(-4)=2,
∴以DE为边的平行四边形的面积与?ABCD面积相等,
∴P点到直线DE的距离为,12÷2=6,
∴P的纵坐标为-3,
把y=-3代入y=-x2-6x-5得-x2-6x-5=-3,解得,x=-3+$\sqrt{7}$或x=-3-$\sqrt{7}$,
当P(-3+$\sqrt{7}$,-3)时,N(-1+$\sqrt{7}$,-3)或(-5+$\sqrt{7}$,-3);
当P(-3-$\sqrt{7}$,-3)时,N(-1-$\sqrt{7}$,-3)或(-5-$\sqrt{7}$,-3);
∴P的坐标为(-3+$\sqrt{7}$,-3)或(-3-$\sqrt{7}$,-3);
N点坐标为:N(-1+$\sqrt{7}$,-3)或(-5+$\sqrt{7}$,-3),N(-1-$\sqrt{7}$,-3)或(-5-$\sqrt{7}$,-3).
点评 本题主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:选择题
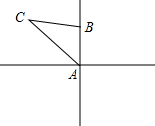 如图,一艘船从某港口A出发,以10海里/小时的速度向正北航行,从港口A处测得一礁石C在北偏西30度的方向上,如果这艘船上午8点从港口A出发10点到达小岛B,此时在小岛B处测得礁石C在北偏西60度方向上,则小岛B与礁石C的距离是( )
如图,一艘船从某港口A出发,以10海里/小时的速度向正北航行,从港口A处测得一礁石C在北偏西30度的方向上,如果这艘船上午8点从港口A出发10点到达小岛B,此时在小岛B处测得礁石C在北偏西60度方向上,则小岛B与礁石C的距离是( )| A. | 40海里 | B. | 30海里 | C. | 20海里 | D. | 10海里 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com