
分析 (1)方程组中的两个方程相加即可求出x+y的值,即可得出关于a的不等式,求出不等式的解集即可;
(2)把a=1代入求出方程组的解,看看是否符合三角形三边关系定理,把符合的求出即可.
解答 解:(1)$\left\{\begin{array}{l}{3x+y=1+a①}\\{x+3y=3②}\end{array}\right.$
①+②得:4x+4y=4+a,
x+y=1+$\frac{1}{4}$a,
∵关于x,y的二元一次方程组$\left\{\begin{array}{l}{3x+y=1+a}\\{x+3y=3}\end{array}\right.$的解满足x+y<2,
∴1+$\frac{1}{4}$a<2,
解得:a<4,
即a的取值范围是a<4;
(2)把a=1代入方程组得:$\left\{\begin{array}{l}{3x+y=2②}\\{x+3y=3②}\end{array}\right.$
①-②×3得:-8y=-7,
y=$\frac{7}{8}$,
①×3-②得:8x=3,
解得:x=$\frac{3}{8}$,
∵$\frac{3}{8}$+$\frac{3}{8}$<$\frac{7}{8}$,
∴等腰三角形的三边只能是$\frac{3}{8}$,$\frac{7}{8}$,$\frac{7}{8}$,
∴此等腰三角形的周长$\frac{3}{8}$+$\frac{7}{8}$+$\frac{7}{8}$=$\frac{17}{8}$.
点评 本题考查了解一元一次不等式,解二元一次方程组,等腰三角形的性质,三角形的三边关系定理的应用,能灵活运用知识点进行计算是解此题的关键,难度适中.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | x=-1,y=1 | B. | x=1,y=-1 | C. | x=-1,y=-1 | D. | x=1,y=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
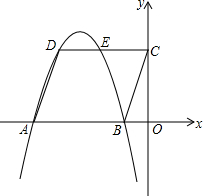 已知:平行四边形ABCD在直角坐标系中的位置如图,O是坐标原点,OB:OC:OA=1:3:5,S□ABCD=12,抛物线经过D、A、B三点.
已知:平行四边形ABCD在直角坐标系中的位置如图,O是坐标原点,OB:OC:OA=1:3:5,S□ABCD=12,抛物线经过D、A、B三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
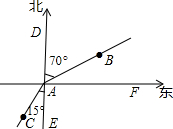 如图,甲从A点出发向北偏东70°方向走50m至点B,乙从A点出发向南偏西15°方向走60m至点C,则∠BAC的度数是( )
如图,甲从A点出发向北偏东70°方向走50m至点B,乙从A点出发向南偏西15°方向走60m至点C,则∠BAC的度数是( )| A. | 85° | B. | 160° | C. | 125° | D. | 105° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com