Question

【题目】如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形．BE交AC于F，AD交CE于G．则下列结论中错误的是（ ）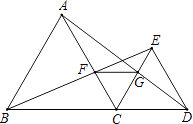

A.AD=BE
B.BE⊥AC
C.△CFG为等边三角形
D.FG∥BC

Answer 1

【答案】B
【解析】解：A、∵△ABC和△CDE均为等边三角形，
∴AC=BC，EC=DC，
∠ACB﹦∠ECD=60°，
∴∠ACD﹦∠ECB，
在△ACD与△BCE中，
∵ ，
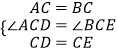∴△ACD≌△BCE（SAS），
∴AD=BE，正确，故本选项错误；
B、根据已知不能推出F是AC中点，即AC和BF不垂直，所以AC⊥BE错误，故本选项正确；
C、△CFG是等边三角形，理由如下：
∵∠ACG=180°﹣60°﹣60°=60°=∠BCA，
∵△ACD≌△BCE，
∴∠CBE=∠CAD，
在△ACG和△BCF中
∵ ，
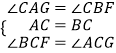∴△ACG≌△BCF（ASA），
∴CG=CH，
又∵∠ACG=60°
∴△CGH是等边三角形，正确，故本选项错误；
D、∵△CFG是等边三角形，
∴∠CFG﹦60°=∠ACB，
∴FG∥BC，正确，故本选项错误；
故选B．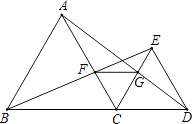

A、证明△ACD≌△BCE即可得出答案；
B、根据等边三角形性质得出AB=BC，只有F为AC中点时，才能推出AC⊥BE．
C、由△ACG≌△BCF，推出CG=CF，根据∠ACG=60°即可证明；
D、根据等边三角形性质得出∠CFG﹦∠ACB=60°，根据平行线的判定推出即可．