
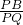 =______;
=______;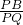 =______;
=______;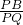 的值,并说明理由.
的值,并说明理由.

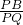 =1,
=1, 在正方形ABCD中,AB∥CD,
在正方形ABCD中,AB∥CD,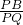 =1,
=1,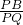 =1,
=1,
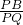 =1.
=1.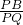 =1;证明图3、4可以仿照这种方法进行.
=1;证明图3、4可以仿照这种方法进行.

科目:初中数学 来源: 题型:
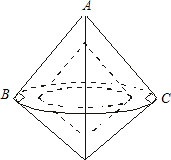 如图,一个直角三角形纸板,其两条直角边长分别为6cm和8cm,小明以纸板的斜边为旋转轴旋转这个三角形纸板形成如图所示的旋转体.请你帮小明推算出这个旋转体的全面积.(π取3.14)
如图,一个直角三角形纸板,其两条直角边长分别为6cm和8cm,小明以纸板的斜边为旋转轴旋转这个三角形纸板形成如图所示的旋转体.请你帮小明推算出这个旋转体的全面积.(π取3.14)查看答案和解析>>
科目:初中数学 来源: 题型:
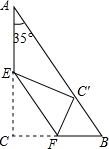 如图是一个直角三角形的纸片,将直角沿EF折叠,使C点落在AB边上,并且使∠EC′A=∠A,那么∠C′FE的度数是( )
如图是一个直角三角形的纸片,将直角沿EF折叠,使C点落在AB边上,并且使∠EC′A=∠A,那么∠C′FE的度数是( )| A、50° | B、45° | C、55° | D、70°第7题图 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com