
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() 、
、![]() 两点在
两点在![]() 上,
上,![]() 、
、![]() 两边分别与
两边分别与![]() 边交于点
边交于点![]() 、
、![]() .固定
.固定![]() 不动,
不动,![]() 从点
从点![]() 与点
与点
B重合的位置出发,沿![]() 边以每秒
边以每秒![]() 个单位的速度向点
个单位的速度向点![]() 运动;同时点
运动;同时点![]() 从点
从点![]() 出发,在折线
出发,在折线![]() 上
上
以每秒![]() 个单位的速度向点
个单位的速度向点![]() 运动.当点
运动.当点![]() 到达点
到达点![]() 时,
时,![]() 和点
和点![]() 同时停止运动.设运动时间为
同时停止运动.设运动时间为![]() (秒).
(秒).

(1)当![]() 时,
时,![]() __________
__________![]() ,
,![]() __________
__________![]() .
.
(2)当![]() 为何值时,
为何值时,![]() 为等腰三角形?请说明理由.
为等腰三角形?请说明理由.
(3)当![]() 为何值时,点
为何值时,点![]() 与点
与点![]() 重合?写出计算过程.
重合?写出计算过程.
【答案】(![]() )
)![]() ,
,![]() ;
;
(![]() )
)![]() 时,
时,![]() 为等腰三角形,明理由见解析;
为等腰三角形,明理由见解析;
(![]() )
)![]() 时,点
时,点![]() 与点
与点![]() 重合,计算过程见解析.
重合,计算过程见解析.
【解析】分析:(1)当t=2,得到BF=2,PF=4,根据BF:BC=HF:AC,即可求出HF,从而得到PH;BE=8,利用Rt△BEG∽Rt△BAC,可求出EG,得到DG;
(2)根据题意得到PD=PE,则BF=t,PF=2t,DF=8,得到PD=DF-PF=8-2t.在Rt△PEF中,利用勾股定理得到4t+36=(8-2t),解得t=![]() .(3)设当△DEF和点P运动的时间是t时,点P与点G重合,此时点P一定在DE边上,DP=DG.根据正切的定义得到tanB=tanD=
.(3)设当△DEF和点P运动的时间是t时,点P与点G重合,此时点P一定在DE边上,DP=DG.根据正切的定义得到tanB=tanD=![]() ,则FH=
,则FH=![]() t,DH=
t,DH=![]() ,得到DG=
,得到DG=![]() ,而DP+DF=2t,于是有2t-8=
,而DP+DF=2t,于是有2t-8=![]() ,即可解得t的值.
,即可解得t的值.
本题解析:
(![]() )∵
)∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∴当![]() 时
时![]() ,∵
,∵![]() ,又∵
,又∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
![]() ,
,![]() ,
,
![]() ,∴当
,∴当![]() 时,
时,![]() .
.
(![]() )只有点
)只有点![]() 在
在![]() 边上运动时,
边上运动时,![]() 才能成为等腰三角形,且
才能成为等腰三角形,且![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
∵![]() ∴
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
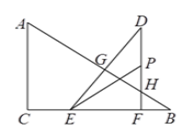
(3)设当![]() 和点
和点![]() 运动的时间是
运动的时间是![]() 时,点
时,点![]() 与点
与点![]() 重合,
重合,
此时,点![]() 在
在![]() 上,
上,![]() ,
,
由已知可得:![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,则此时点
,则此时点![]() 在
在![]() 上,
上,
当![]() 时,点
时,点![]() 与点
与点![]() 重合.
重合.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】如图是根据宝塔山公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(﹣400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向右转90°后直行400m到达樱花园C,则点C的坐标是 . 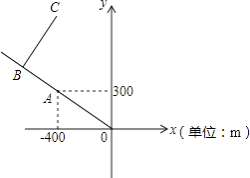
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC≌△DCB,若BC=10cm,AB=6cm,AC=7cm,则CD为( )
A. 10cm B. 7cm C. 6cm D. 6cm或7cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)设![]() ,求该抛物线的解析式;
,求该抛物线的解析式;
(2)在⑴中,若点![]() 为直线
为直线![]() 下方抛物线上一动点,当⊿
下方抛物线上一动点,当⊿![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)是否存在整数![]() 使得
使得![]() 和
和![]() 同时成立,请证明你的结论.
同时成立,请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初步测算,2015年海宁市全年实现地区生产总值700.23亿元,比上年增长6.7%.其中700.23亿用科学记数法表示为( )
A.700.23×108
B.70.023×109
C.7.0023×1010
D.7.0023×109
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com