
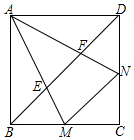
 如图,在正方形ABCD中,点M,N分别在边BC,CD上,且∠MAN=45°,AM,AN分别与对角线BD交于点E,F,若EM=$\sqrt{10}$,CM=2BM,则EF的长为5$\sqrt{2}$.
如图,在正方形ABCD中,点M,N分别在边BC,CD上,且∠MAN=45°,AM,AN分别与对角线BD交于点E,F,若EM=$\sqrt{10}$,CM=2BM,则EF的长为5$\sqrt{2}$. 分析 连接AC,根据正方形的性质得到∠ACM=∠ADF=∠CAD=45°,得到AC=$\sqrt{2}$AD,推出△MAC∽△FAD,根据相似三角形的性质得到AM=$\sqrt{2}$AF,设MB=x,则CM=2x,AB=3x,勾股定理AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\sqrt{10}$x,得到AF=$\sqrt{5}$x,然后根据勾股定理即可得到结论.
解答 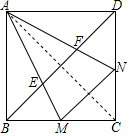 证明:连接AC,
证明:连接AC,
∵四边形ABCD是正方形
∴∠ACM=∠ADF=∠CAD=45°,
∴AC=$\sqrt{2}$AD,
∵∠MAN=45°,
∴∠MAN=∠CAD,
∴∠MAN-∠CAN=∠CAD-∠CAN,
∴∠MAC=∠FAD,
∴△MAC∽△FAD,
∴AN:AF=AC:AD,
∴AM:AF=$\sqrt{2}$:1,
∴AM=$\sqrt{2}$AF,
∵CM=2BM,
∴设MB=x,则CM=2x,AB=3x,
∴AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\sqrt{10}$x,
∴AF=$\sqrt{5}$x,
∵∠EAF=∠∠MBE=45°,
∠BEM=∠AEF,
∴△AEF∽△BME,
∴$\frac{EF}{EM}=\frac{AF}{BM}$,即$\frac{EF}{\sqrt{10}}$=$\frac{\sqrt{5}x}{x}$,
∴EF=5$\sqrt{2}$.
故答案为:5$\sqrt{2}$.
点评 此题考查了相似三角形的判定与性质、等腰直角三角形的性质以及正方形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | x2+$\frac{1}{x}$ | B. | ax2+bx+c=0 | C. | (x-1)(x+2)=1 | D. | 3x2-2xy-5y2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
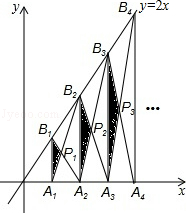 如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则S2016=$\frac{201{6}^{2}}{4033}$.
如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、B2A3、…、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则S2016=$\frac{201{6}^{2}}{4033}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com