
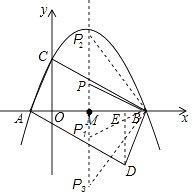
【题目】如图,抛物线y=﹣ ![]() x2+
x2+ ![]() x+2与x轴交于点A,B,与y轴交于点C.
x+2与x轴交于点A,B,与y轴交于点C.
(1)试求A,B,C的坐标;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
【答案】
(1)
解:当y=0时,0=﹣ ![]() x2+
x2+ ![]() x+2,
x+2,
解得:x1=﹣1,x2=4,
则A(﹣1,0),B(4,0),
当x=0时,y=2,
故C(0,2)
(2)
解:①过点D作DE⊥x轴于点E,
∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴DE=2,AO=BE=1,OM=ME=1.5,
∴D(3,﹣2);
②∵将△ABC绕AB中点M旋转180°,得到△BAD,
∴AC=BD,AD=BC,
∴四边形ADBC是平行四边形,
∵AC= ![]() =
= ![]() ,BC=
,BC= ![]() =2
=2 ![]() ,
,
AB=5,
∴AC2+BC2=AB2,
∴△ACB是直角三角形,
∴∠ACB=90°,
∴四边形ADBC是矩形
(3)
解:由题意可得:BD= ![]() ,AD=2
,AD=2 ![]() ,
,
则 ![]() =
= ![]() ,
,
当△BMP∽△ADB时,
![]() =
= ![]() =
= ![]() ,
,
可得:BM=2.5,
则PM=1.25,
故P(1.5,1.25),
当△BMP1∽△ABD时,
P1(1.5,﹣1.25),
当△BMP2∽△BDA时,
可得:P2(1.5,5),
当△BMP3∽△BDA时,
可得:P3(1.5,﹣5),
综上所述:点P的坐标为:(1.5,1.25),(1.5,﹣1.25),(1.5,5),(1.5,﹣5)
【解析】(1)直接利用y=0,x=0分别得出A,B,C的坐标;(2)①利用旋转的性质结合三角形各边长得出D点坐标;②利用平行四边形的判定方法结合勾股定理的逆定理得出四边形ADBC的形状;(3)直接利用相似三角形的判定与性质结合三角形各边长进而得出答案.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】小明乘出租车去体育场,有两条路线可供选择:路线一的全程是25千米,但交通比较拥堵,路线二的全程是36千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路线一少用10分钟到达.求小明走路线一时的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
x(单位:台) | 10 | 20 | 30 |
y(单位:万元∕台) | 60 | 55 | 50 |
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求该机器的生产数量;
(3)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价﹣成本) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是 ![]() .
.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生最喜欢的球类情况,随机抽取了八年级部分学生进行问卷调查,调查分为最喜欢篮球、乒乓球、足球、排球共四种情况,每名同学选且只选一项,现将调查结果绘制成如下所示的两幅统计图. 
请结合这两幅统计图,解决下列问题:
(1)在这次问卷调查中,一共抽取了名学生;
(2)请补全条形统计图;
(3)若该校八年级共有300名学生,请你估计其中最喜欢排球的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=﹣x2+(m﹣1)x+m(m为常数).
(1)该函数的图象与x轴公共点的个数是 .
A.0
B.1
C.2
D.1或2
(2)求证:不论m为何值,该函数的图象的顶点都在函数y=(x+1)2的图象上.
(3)当﹣2≤m≤3时,求该函数的图象的顶点纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG.点F,G分别在边AD,BC上,连结OG,DG.若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( ) 
A.CD+DF=4
B.CD﹣DF=2 ![]() ﹣3
﹣3
C.BC+AB=2 ![]() +4
+4
D.BC﹣AB=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com