
【题目】已知函数y=﹣x2+(m﹣1)x+m(m为常数).
(1)该函数的图象与x轴公共点的个数是 .
A.0
B.1
C.2
D.1或2
(2)求证:不论m为何值,该函数的图象的顶点都在函数y=(x+1)2的图象上.
(3)当﹣2≤m≤3时,求该函数的图象的顶点纵坐标的取值范围.
【答案】
(1)D
(2)证明:y=﹣x2+(m﹣1)x+m=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
把x= ![]() 代入y=(x+1)2得:y=(
代入y=(x+1)2得:y=( ![]() +1)2=
+1)2= ![]() ,
,
则不论m为何值,该函数的图象的顶点都在函数y=(x+1)2的图象上
(3)解:设函数z= ![]() ,
,
当m=﹣1时,z有最小值为0;
当m<﹣1时,z随m的增大而减小;
当m>﹣1时,z随m的增大而增大,
当m=﹣2时,z= ![]() ;当m=3时,z=4,
;当m=3时,z=4,
则当﹣2≤m≤3时,该函数图象的顶点坐标的取值范围是0≤z≤4
【解析】解:(1)∵函数y=﹣x2+(m﹣1)x+m(m为常数), ∴△=(m﹣1)2+4m=(m+1)2≥0,
则该函数图象与x轴的公共点的个数是1或2,
故选D;
【考点精析】根据题目的已知条件,利用二次函数的性质和抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D是AC的中点,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E. 
(1)若∠A+∠CDB=90°,求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+
x2+ ![]() x+2与x轴交于点A,B,与y轴交于点C.
x+2与x轴交于点A,B,与y轴交于点C.
(1)试求A,B,C的坐标;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D、F分别在边AB、AC上. 
(1)求证:△BDE∽△CEF;
(2)当点E移动到BC的中点时,求证:FE平分∠DFC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲、乙两个家庭有了各自的规划,假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2015次操作后得到的折痕D2014E2014到BC的距离记为h2015 . 若h1=1,则h2015的值为( ) 
A.![]()
B.![]()
C.1﹣ ![]()
D.2﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | 6 |
X(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
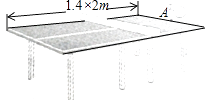
(1)当t为何值时,乒乓球达到最大高度?
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后,y与x满足y=a(x﹣3)2+k.
①用含a的代数式表示k;
②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC=4cm,把它沿着对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形EMCN的面积之比为( ) 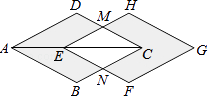
A.4:3
B.3:2
C.14:9
D.17:9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com