
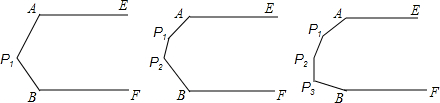
分析 连接AB,如图1、图2、图3,可利用平行线的性质和多边形的内角和定理求出∠EAP1+∠P1+∠P1BF、∠EAP1+∠P1+∠P2+∠P2BF、∠EAP1+∠P1+∠P2+∠P3+∠P3BF的度数,而小王、小李、小徐转过的角度又分别是这些角补角的和,从而可求出他们转过的角度,问题得以解决,
解答 解:小李说法正确.
①连接AB,如图1,
∵AE∥BF,
∴∠EAB+∠ABF=180°.
∵∠P1AB+∠P1+∠P1BA=180°,
∴∠EAP1+∠P1+∠P1BF=360°.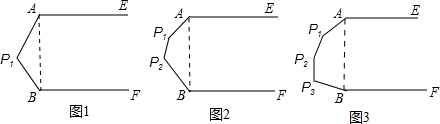
∴小王转过的角度为180°-∠EAP1+180°-∠P1+180°-∠P1BF
=540°-(∠EAP1+∠P1+∠P1BF)=540°-360°
=180°;
②连接AB,如图2,
∵AE∥BF,
∴∠EAB+∠ABF=180°.
∵∠P1AB+∠P1+∠P2+∠P2BA=360°,
∴∠EAP1+∠P1+∠P2+∠P2BF=540°.
∴小李转过的角度为180°-∠EAP1+180°-∠P1+180°-∠P2+180°-∠P2BF
=720°-(∠EAP1+∠P1+∠P2+∠P2BF)
=720°-540°
=180°;
③连接AB,如图3,
∵AE∥BF,
∴∠EAB+∠ABF=180°.
∵∠P1AB+∠P1+∠P2+∠P3+∠P3BA=540°,
∴∠EAP1+∠P1+∠P2+∠P3+∠P3BF=720°.
∴小徐转过的角度为180°-∠EAP1+180°-∠P1+180°-∠P2+180°-∠P3+180°-∠P3BF
=900°-(∠EAP1+∠P1+∠P2+∠P3+∠P3BF)
=900°-720°
=180°;
综上所述:他们三人转过的角度一样多,小李说法正确.
点评 本题主要考查了平行线的性质、多边形的内角和定理、邻补角等知识,弄清三人转过的角度与图中角的关系,是解决本题的关键.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | 30米 | B. | 40米 | C. | 25米 | D. | 35米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x+6=-3变形为2x=-3+6 | B. | $\frac{x+3}{3}$-$\frac{x+1}{2}$=1变形为2x+6=-3x+3=6 | ||
| C. | $\frac{2}{5}$x-$\frac{2}{3}$x=$\frac{1}{3}$变形为6x-10x=5 | D. | $\frac{3}{5}$x=2(x-1)+1变形为3x=10(x-1)+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
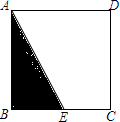 某人定制了一批如图所示的地砖,每块地砖都是边长为(x+3y)米的正方形,点E在正方形ABCD的边BC上,EC=(x+y)米,已知x+3y=5米,x+2y=4米,求四边形AECD的面积.
某人定制了一批如图所示的地砖,每块地砖都是边长为(x+3y)米的正方形,点E在正方形ABCD的边BC上,EC=(x+y)米,已知x+3y=5米,x+2y=4米,求四边形AECD的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com