练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积= ACBD，其中正确的结论有（ ）
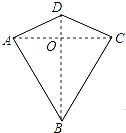
    A.0个
    B.1个
    C.2个
    D.3个

    【答案】D
    【解析】解：在△ABD与△CBD中， ，
    ∴△ABD≌△CBD（SSS），
    故①正确；
    ∴∠ADB=∠CDB，
    在△AOD与△COD中，
    ，
    ∴△AOD≌△COD（SAS），
    ∴∠AOD=∠COD=90°，AO=OC，
    ∴AC⊥DB，
    故②正确；
    四边形ABCD的面积= = ACBD，
    故③正确；
    故选D．
    先证明△ABD与△CBD全等，再证明△AOD与△COD全等即可判断．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】两条直线都与第三条直线相交，∠1和∠2是内错角，∠3和∠2是邻补角．

    (1)根据上述条件，画出符合题意的图形；

    (2)若∠1∶∠2∶∠3＝1∶2∶3，求∠1，∠2，∠3的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀平均分成4 个小长方形，然后按图2的形状拼成一个正方形．

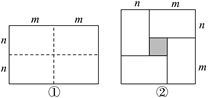
    (1)图2中阴影部分的面积为 ；

    (2)观察图2，请你写出式子(m＋n)2，(m－n)2，mn之间的等量关系： ；

    (3)若x＋y＝－6，xy＝2.75，求x－y的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（ ，1）在反比例函数y= 的图象上．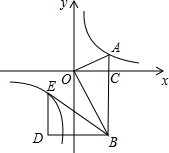

    （1）求反比例函数y= 的表达式；
    （2）在x轴的负半轴上存在一点P，使得S△AOP= S△AOB ， 求点P的坐标；
    （3）若将△BOA绕点B按逆时针方向旋转60°得到△BDE．直接写出点E的坐标，并判断点E是否在该反比例函数的图象上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为x= ，且经过点（2，0），有下列说法：①abc＜0；②a+b=0；③a﹣b+c=0；④若（0，y1），（1，y2）是抛物线上的两点，则y1=y2 ． 上述说法正确的是（ ）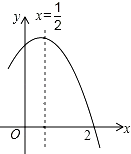
    A.①②③④
    B.③④
    C.①③④
    D.①②

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在下面的方格纸中，找出互相平行的线段，并用符号表示出来：__________，__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0）、B（3，0）．

    （1）求b、c的值；
    （2）如图1直线y=kx+1（k＞0）与抛物线第一象限的部分交于D点，交y轴于F点，交线段BC于E点．求 的最大值；
    （3）如图2，抛物线的对称轴与抛物线交于点P、与直线BC相交于点M，连接PB．问在直线BC下方的抛物线上是否存在点Q，使得△QMB与△PMB的面积相等？若存在，求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动，点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动，在直角三角形ABC中，∠A＝90°，若AB＝16厘米，AC＝12厘米，BC＝20厘米，如果P、Q同时出发，用t（秒）表示移动时间，那么：

    （1）如图1，若P在线段AB上运动，Q在线段CA上运动，试求出t为何值时，QA＝AP

    （2）如图2，点Q在CA上运动，试求出t为何值时，三角形QAB的面积等于三角形ABC面积的；

    （3）如图3，当P点到达C点时，P、Q两点都停止运动，试求当t为何值时，线段AQ的长度等于线段BP的长的

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着全国各地空气出现严重污染，PM2.5屡屡爆表，我国多个城市发生雾霾天气，越来越多的人开始关注一个原本陌生的术语﹣PM2.5．某校九年级共有1000名学生，团委准备调查他们对“PM2.5”知识的了解程度．
    （1）在确定调查方式时，团委设计了以下三种方案： 方案一：调查九年级部分女生；
    方案二：调查九年级部分男生；
    方案三：到九年级每个班去随机调查一定数量的学生．
    请问其中最具有代表性的一个方案是；
    （2）团委采用了最具有代表性的调查方案，并用收集到的数据绘制出两幅不完整的统计图，请你根据图中信息，将其补充完整；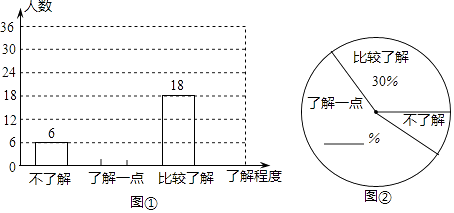
    （3）请你估计该校九年级约有多少名学生比较了解“PM2.5”的知识．

    查看答案和解析>>

    同步练习册答案