
【题目】如图,E、F为菱形ABCD对角线上的两点,∠ADE=∠CDF,要判定四边形BFDE是正方形,需添加的条件是( )
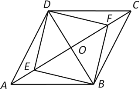
A.AE=CFB.OE=OFC.∠EBD=45°D.∠DEF=∠BEF
【答案】C
【解析】
从对角线的角度看,一个四边形需满足其两条对角线垂直、平分且相等才能判定是正方形,由于菱形的对角线已经垂直,所以要判定四边形BFDE是正方形,只需证明BD和EF相等且平分,据此逐项判断即可.
解:∵四边形ABCD是菱形,∴AO=CO,BO=DO,AC⊥BD,
A、若AE=CF,则OE=OF,但EF与BD不一定相等,所以不能判定四边形BFDE是正方形,本选项不符合题意;
B、若OE=OF,同样EF与BD不一定相等,所以不能判定四边形BFDE是正方形,本选项也不符合题意;
C、若∠EBD=45°,∵∠BOE=90°,∴∠BEO=45°,∴OE=OB,
∵AD=CD,∴∠DAE=∠DCF,又∵∠ADE=∠CDF,
∴△ADE≌△CDF(ASA),∴AE=CF,∴OE=OF,
∴EF=BD,∴四边形BFDE是正方形,本选项符合题意;
D、若∠DEF=∠BEF,由C选项的证明知OE=OF,但不能证明EF与BD相等,所以不能判定四边形BFDE是正方形,本选项不符合题意.
故选:C.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
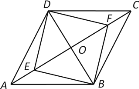
【题目】平行四边形ABCD中,∠A=60°,AB=2AD,BD的中垂线分别交AB,CD于点E,F,垂足为O.
(1)求证:OE=OF;
(2)若AD=6,求tan∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水务部门为加强防汛工作,决定对某水库大坝进行加固.原大坝的横截面是梯形ABCD,如图所示,已知迎水面AB的长为10米,∠B=60°,背水面DC的长度为![]() 米,加固后大坝的横截面是梯形ABED,CE的长为5米.
米,加固后大坝的横截面是梯形ABED,CE的长为5米.

(1)已知需加固的大坝长为100米,求需要填方多少立方米;
(2)求新大坝背水面![]() 的坡度.(计算结果保留根号)。
的坡度.(计算结果保留根号)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠C=90°,∠B=30°,以点 A 为圆心,任意长为半径画弧分别交 AB,AC 于点M 和 N,再分别以 M,N 为圆心,大于![]() MN的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2,正确的序号是_____.
MN的长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点D,则下列说法中:①AD 是∠BAC 的平分线;②点 D 在线段 AB 的垂直平分线上;③S△DAC:S△ABC=1:2,正确的序号是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
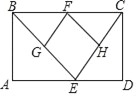
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
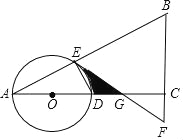
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,以OA为半径的圆分别交AB、AC于点E、D,在BC的延长线上取点F,使得BF=EF.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若∠A=30°,求证:DG=![]() DA;
DA;
(3)若∠A=30°,且图中阴影部分的面积等于2![]() ,求⊙O的半径的长.
,求⊙O的半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知点C周围200 m范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600 m到达B处,测得C在点B的北偏西60°方向上.
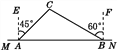
(1)MN是否穿过原始森林保护区?为什么?(参考数据: ![]() ≈1.732)
≈1.732)
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,O为菱形ABCD的对称中心,已知C(2,0),D(0,﹣1),N为线段CD上一点(不与C、D重合).
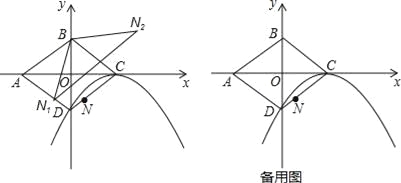
(1)求以C为顶点,且经过点D的抛物线解析式;
(2)设N关于BD的对称点为N1,N关于BC的对称点为N2,求证:△N1BN2∽△ABC;
(3)求(2)中N1N2的最小值;
(4)过点N作y轴的平行线交(1)中的抛物线于点P,点Q为直线AB上的一个动点,且∠PQA=∠BAC,求当PQ最小时点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016甘肃省白银市)如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com