
A. | B. | C. | D. |
科目:初中数学 来源:不详 题型:解答题
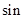 20°=0.3420,
20°=0.3420,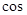 20°=0.9397,
20°=0.9397,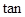 20°=0.3640)
20°=0.3640) 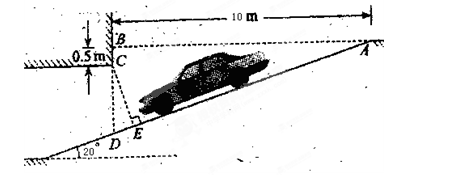
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
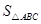 =
= AB·CD,
AB·CD,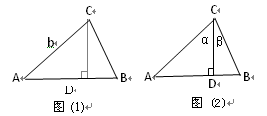
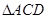 中,
中,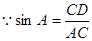 ,
,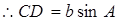
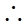
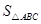 =
=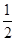 bc·sin∠A.
bc·sin∠A.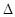 ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.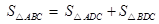 , 由公式①,得
, 由公式①,得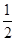 AC·BC·sin(α+β)=
AC·BC·sin(α+β)= 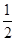 AC·CD·sinα+
AC·CD·sinα+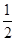 BC·CD·sinβ,
BC·CD·sinβ,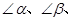
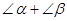 的正弦或余弦函数表示(直接写出结果).
的正弦或余弦函数表示(直接写出结果).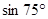 =_________________________
=_________________________查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com