
分析 (1)根据分式的加法法则,从左向右计算即可;
(2)首先把每个分式化成两个分式相减的形式,计算即可;
(3)把前两个和后两个分别计算,然后再根据分式的加减法法则计算即可.
解答 解:(1)$\frac{1}{a-b}$+$\frac{1}{a+b}$+$\frac{2a}{{a}^{2}+{b}^{2}}$+$\frac{4{a}^{3}}{{a}^{4}+{b}^{4}}$
=$\frac{a+b+a-b}{(a+b)(a-b)}$+$\frac{2a}{{a}^{2}+{b}^{2}}$+$\frac{4{a}^{3}}{{a}^{4}+{b}^{4}}$
=$\frac{2a({a}^{2}+{b}^{2})+2a({a}^{2}-{b}^{2})}{({a}^{2}-{b}^{2})({a}^{2}+{b}^{2})}$+$\frac{4{a}^{3}}{{a}^{4}+{b}^{4}}$
=$\frac{4{a}^{3}}{{a}^{4}-{b}^{4}}$+$\frac{4{a}^{3}}{{a}^{4}+{b}^{4}}$
=$\frac{4{a}^{3}({a}^{4}+{b}^{4})+4{a}^{3}({a}^{4}-{b}^{4})}{({a}^{4}-{b}^{4})({a}^{4}+{b}^{4})}$
=$\frac{8{a}^{7}}{({a}^{8}-{b}^{8})}$;
(2)$\frac{1}{x(x+1)}$+$\frac{1}{(x+1)(x+2)}$+$\frac{1}{(x+2)(x+3)}$+…+$\frac{1}{(x+99)(x+100)}$
=$\frac{1}{x}-\frac{1}{x+1}$+$\frac{1}{x+1}-\frac{1}{x+2}$+$\frac{1}{x+2}-\frac{1}{x+3}$+…+$\frac{1}{x+99}-\frac{1}{x+100}$
=$\frac{1}{x}-\frac{1}{x+100}$
=$\frac{x+100-x}{x(x+100)}$
=$\frac{100}{x(x+100)}$;
(3)$\frac{1}{1+a}$+$\frac{1}{1-a}$+$\frac{1}{(1+a)(1+2a)}$+$\frac{1}{(1-a)(1-2a)}$
=$\frac{1-a+1+a}{(1+a)(1-a)}$+$\frac{(1-a)(1-2a)+(1+a)(1+2a)}{(1+a)(1+2a)(1-a)(1-2a)}$
=$\frac{2}{(1+a)(1-a)}$+$\frac{2+4{a}^{2}}{(1+a)(1-a)(1+2a)(1-2a)}$
=$\frac{2}{1-{a}^{2}}$+$\frac{2+4{a}^{2}}{(1-{a}^{2})(1-4{a}^{2})}$
=$\frac{2(1-4{a}^{2})+2+4{a}^{2}}{(1-{a}^{2}()1-4{a}^{2})}$
=$\frac{4(1-{a}^{2})}{(1-{a}^{2})(1-4{a}^{2})}$
=$\frac{4}{1-4{a}^{2}}$.
点评 本题考查了分式的加减法法则、整体思想方法的运用;熟练掌握分式的加减法法则是解决问题的关键.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
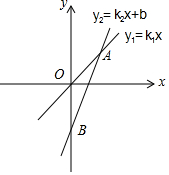 如图,正比例函数y1=k1x与一次函数y2=k2x+b的图象相交于A(3,4),直线y2=k2x+b与y轴相交于点B,OB=OA.
如图,正比例函数y1=k1x与一次函数y2=k2x+b的图象相交于A(3,4),直线y2=k2x+b与y轴相交于点B,OB=OA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
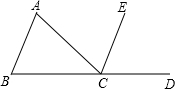 如图,△ABC中,AC=BC,点D在BC的延长线上,CE∥AB.试说明:CE是∠ACD的角平分线.
如图,△ABC中,AC=BC,点D在BC的延长线上,CE∥AB.试说明:CE是∠ACD的角平分线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com