为发展“低碳经济”,某单位进行技术革新,让可再生资源重新利用.从今年1月1日开始,该单位每月再生资源处理量y(吨)与月份x之间成如下一次函数关系:
月处理成本z(元)与每月再生资源处理量y(吨)之间的函数关系可近似地表示为:z=
y
2-20y+700,每处理一吨再生资源得到的新产品的售价定为100元.
(1)直接写出该单位每月再生资源处理量y(吨)与月份x之间关系式,月处理成本z(元)与月份x之间关系式.
(2)设该单位每月获得利润S元,写出S与x的关系式,并说明哪个月获得利润最大?最大是多少?
(3)随着人们环保意识的增加,该单位需求的可再生资源数量受限.今年三、四月份的再生资源处理量都比二月份减少了m%,该新产品的产量也随之减少,其售价都比二月份的售价增加了0.6m%.五月份,该单位得到国家科委的技术支持,使月处理成本比二月份的降低了20%.如果该单位在保持三月份的再生资源处理量和新产品售价的基础上,其利润是二月份的利润的一样,求m.( m保留整数)
(
≈12.53,
≈12.49
,≈12.57)

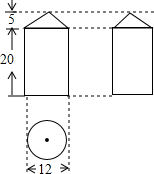 如图是某几何体的三视图.
如图是某几何体的三视图.