
【题目】如图,在△ABC中,AB=AC,以AB为直径的![]() 与边BC,AC分别交于D、E,DF是
与边BC,AC分别交于D、E,DF是![]() 的切线,交AC于点F.
的切线,交AC于点F.
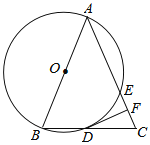
(1)求证:DF⊥AC;
(2)若AE=4,DF=3,求![]() 的半径.
的半径.
【答案】(1)证明见详解
(2)半径为![]()
【解析】
(1)连接OD,作OG⊥AC于点G,推出∠ODB=∠C;然后证明DF⊥AC,∠DFC=90°,推出∠ODF=∠DFC=90°,即可证明;
(2)过O作OG⊥AC,利用垂径定理和矩形的性质,勾股定理解答即可.
(1)证明:如图,连接OD,作OG⊥AC于点G,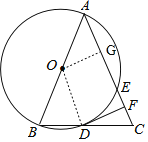 ,
,
∵OB=OD,
∴∠ODB=∠B,
又∵AB=AC,
∴∠C=∠B,
∴∠ODB=∠C,
∴AC//OD
∵DF是![]() 的切线
的切线
即:DF⊥OD,
∴∠ODF=∠DFC=90°,
∴DF⊥AC;
(2)过O作OG⊥AC,
由垂径定理可知:OG垂直平分AE,
∴∠AGO=90°,AG=2,
由(1)可知:四边形ODFG为矩形,
∴OG=DF=3,
∴在Rt△AGO中,![]()
∴![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两名自行车运动员同时从A地出发到B地,在直线公路上进行骑自行车训练.如图,反映了甲、乙两名自行车运动员在公路上进行训练时的行驶路程S(千米)与行驶时间t(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时乙在甲前10千米;④3小时时甲追上乙.其中正确的个数有( )
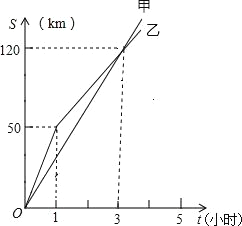
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“诵读诗词经典,弘扬传统文化”诗词诵读活动,为了解八年级学生在这次活动中的诗词诵背情况,随机抽取了30名八年级学生,调查“一周诗词诵背数量调查结果如表所示.
一周诗词诵背数量(首) | 2 | 3 | 4 | 5 | 6 | 7 |
人数(人) | 1 | 3 | 5 | 9 | 10 | 2 |
(1)计算这30人平均每人一周诵背诗词多少首;
(2)该校八年级共有600名学生参加了这次活动,在这次活动中,估计八年级学生中一周诵背诗词6首以上(含6首)的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(k﹣1)x2+(2k﹣3)x+k+1=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,抛物线的顶点为P,对称轴为直线
与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,抛物线的顶点为P,对称轴为直线![]() ,且OC=3OA.
,且OC=3OA.
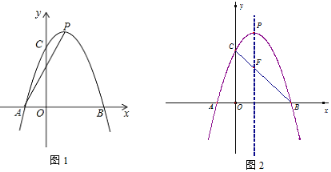
(1)求抛物线的解析式;
(2)点D(2,m)在抛物线上,点E在直线AP上,使DE⊥OE,求点E的横坐标;
(3)如图2,连接BC与抛物线的对称轴交于点F,在抛物线上是否存在点G,使△GPF与△GBF的面积相等,若存在,求出点G坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)过点D(0,![]() )作x轴的平行线交抛物线于E,F两点,求EF的长;
)作x轴的平行线交抛物线于E,F两点,求EF的长;
(3)当y≤![]() 时,直接写出x的取值范围是 .
时,直接写出x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
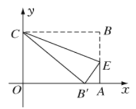
【题目】如图,在平面直角坐标系中放入一个一边长OC为9的矩形纸片ABCO,将纸片翻折后,点B恰好落在x轴上,记为点B′,折痕为CE,已知tan∠OB′C=![]() .
.
(1)求点B′的坐标;
(2)求折痕CE所在直线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大美武汉·诗意江城”,某校数学兴趣小组就“最想去的武汉市旅游景点”随机调查了本校3000名学生中的部分学生,提供四个景点选择:A、黄鹤楼;B、东湖海洋世界;C、极地海洋世界;D、欢乐谷.要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:
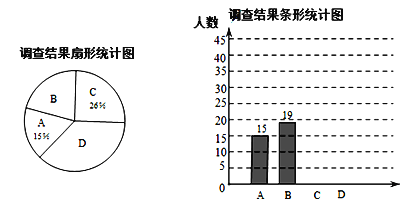
请根据图中提供的信息,解答下列问题:
(1) 一共调查了学生___________人
(2) 扇形统计图中表示“最想去的景点D”的扇形圆心角为___________度
(3) 如果A、B、C、D四个景点提供给学生优惠门票价格分别为20元、30元、40元、60元,根据以上的统计估计全校学生到对应的景点所需要门票总价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
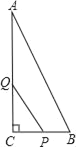
【题目】如图,△ABC中,∠C=90°,AC=16cm,BC=8cm,一动点P从点C出发沿着CB方向以2cm/s的速度运动,另一动点Q从A出发沿着AC边以4cm/s的速度运动,P、Q两点同时出发,运动时间为t(s).
(1)若△PCQ的面积是△ABC面积的![]() ,求t的值?
,求t的值?
(2)△PCQ的面积能否与四边形ABPQ面积相等?若能,求出t的值;若不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com