
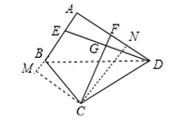
已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.(1)如图1,若四边形ABCD是矩形,且DE⊥CF.则
 (填“<”或“=”或“>”);
(填“<”或“=”或“>”);
(2)如图2,若四边形ABCD是平行四边形,试探究:
当∠B与∠EGC满足什么关系时,使得 =
= 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图3,若BA=BC= 3,DA=DC= 4,∠BAD= 90°,DE⊥CF.则 的值为 .
的值为 .

图1 图2 图3
(1)=;(2)∠B=∠EGC;(3)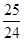 .
.
【解析】
试题分析:(1)根据矩形性质得出∠A=∠FDC=90°,求出∠CFD=∠AED,证出△AED∽△DFC即可;
(2)当∠B+∠EGC=180°时,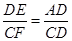 成立,证△DFG∽△DEA,得出
成立,证△DFG∽△DEA,得出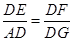 ,证△CGD∽△CDF,得出
,证△CGD∽△CDF,得出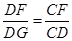 ,即可得出答案;
,即可得出答案;
(3)过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,△BAD≌△BCD,推出∠BCD=∠A=90°,证△BCM∽△DCN,求出CM=x,在Rt△CMB中,由勾股定理得出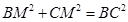 ,代入得出方程
,代入得出方程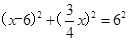 ,求出CN=
,求出CN=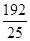 ,证出△AED∽△NFC,即可得出答案.
,证出△AED∽△NFC,即可得出答案.
试题解析:(1)证明:∵四边形ABCD是矩形,
∴∠A=∠FDC=90°,
∵CF⊥DE,
∴∠DGF=90°,
∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,
∴∠CFD=∠AED,
∵∠A=∠CDF,
∴△AED∽△DFC,
∴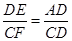 ,即
,即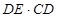 =
=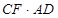 .
.
(2)当∠B+∠EGC=180°时,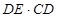 =
=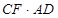 成立.
成立.
证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AD∥BC,
∴∠B+∠A=180°,
∵∠B+∠EGC=180°,
∴∠A=∠EGC=∠FGD,
∵∠FDG=∠EDA,
∴△DFG∽△DEA,
∴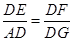 ,
,
∵∠B=∠ADC,∠B+∠EGC=180°,∠EGC+∠DGC=180°,
∴∠CGD=∠CDF,
∵∠GCD=∠DCF,
∴△CGD∽△CDF,
∴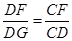 ,
,
∴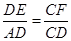 ,
,
∴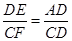 ,
,
即当∠B+∠EGC=180°时,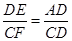 成立.
成立.
(3)解: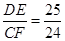 .
.
理由是:过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,
∵AB⊥AD,
∴∠A=∠M=∠CNA=90°,
∴四边形AMCN是矩形,
∴AM=CN,AN=CM,
∵在△BAD和△BCD中
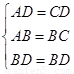
∴△BAD≌△BCD(SSS),
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC+∠CBM=180°,
∴∠CBM=∠ADC,
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
∴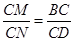 ,
,
∴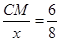
∴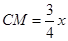
在Rt△CMB中,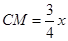 ,BM=AM﹣AB=x﹣6,由勾股定理得:
,BM=AM﹣AB=x﹣6,由勾股定理得: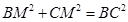 ,
,
∴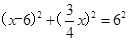 ,
,
解得 x=0(舍去),x=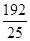
∴CN=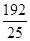 ,
,
∵∠A=∠FGD=90°,
∴∠AED+∠AFG=180°,
∵∠AFG+∠NFC=180°,
∴∠AED=∠CFN,
∵∠A=∠CNF=90°,
∴△AED∽△NFC,
∴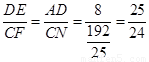
考点: 相似三角形综合题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、2个 | B、3个 | C、4个 | D、6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 年 份 | 2001 | 2002 | 2003 | 2004 | … |
| 财政收入 单位(亿元) |
10 | 10.5 | 12 | 14.5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,
如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com