
| A. | 36° | B. | 45° | C. | 36°或45° | D. | 36°或45°或72° |
分析 △ACD和△ABD都是等腰三角形,但没有说具体的边相等,所以应分情况讨论.
(1)AD=BD,DC=AD,那么△ADB和△ADC是全等三角形,可求得∠ADC,进一步得到∠C;
(2)AB=BD,CD=AD,那么∠B=∠C=∠DAC,∠BAD=∠BDA=2∠C,然后用∠C表示出△ABC的内角和,即可求得5∠C,进一步得到∠C.
解答 解:应分两种情况:
(1)如图: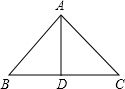
AD=BD,DC=AD,那么△ADB和△ADC是全等三角形,可求得∠ADC=90°,那么∠C=45°;
(2)如图: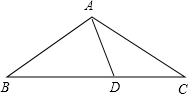
AB=BD,CD=AD,那么∠B=∠C=∠DAC,∠BAD=∠BDA=2∠C,然后用∠C表示出△ABC的内角和,即可求得5∠C=180°,那么∠C=36°.
故选:C.
点评 本题考查了全等三角形的判定和性质及等腰三角形的性质;本题的易错点在于判断此题应分情况讨论,难点在于画出图形,得到各种情况里所求的角的关系.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,AD⊥BC,EF⊥BC,G为线段AB上的一个动点.
已知,如图,AD⊥BC,EF⊥BC,G为线段AB上的一个动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM,CN,MN,若AB=2$\sqrt{2}$,BC=2$\sqrt{3}$,求图中阴影部分的面积.
如图,矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM,CN,MN,若AB=2$\sqrt{2}$,BC=2$\sqrt{3}$,求图中阴影部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
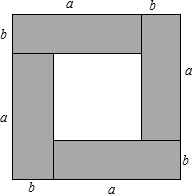 数学结合是一种重要的数学思想,借助这种方法我们可以将抽象的数学知识变得直观且具有可操作性,初中数学里的代数公式,有很多都可以通过表示几何图形面积的方法进行推导和验证,例如完全平方公式.下面我们进行类似的探究:
数学结合是一种重要的数学思想,借助这种方法我们可以将抽象的数学知识变得直观且具有可操作性,初中数学里的代数公式,有很多都可以通过表示几何图形面积的方法进行推导和验证,例如完全平方公式.下面我们进行类似的探究:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com