
如图,已知直线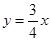 ,点A的坐标是(4,0),点D为x轴上位于点A右边的某一点,点B为直线
,点A的坐标是(4,0),点D为x轴上位于点A右边的某一点,点B为直线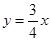 上的一点,以点A、B、D为顶点作正方形.
上的一点,以点A、B、D为顶点作正方形.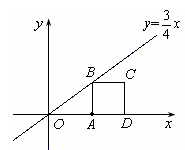
(1)若图①仅看作符合条件的一种情况,求出所有符合条件的点D的坐标;
(2)在图①中,若点P以每秒1个单位长度的速度沿直线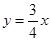 从点O移动到点B,与此同时点Q以相同的速度从点A出发沿着折线A-B-C移动,当点P到达点B时两点停止运动.试探究:在移动过程中,△PAQ的面积最大值是多少?
从点O移动到点B,与此同时点Q以相同的速度从点A出发沿着折线A-B-C移动,当点P到达点B时两点停止运动.试探究:在移动过程中,△PAQ的面积最大值是多少?
(1)(7,0)或(16,0)或(28,0);(2)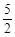 或3;
或3;
解析试题分析:(1)仔细分析题意,正确画出图形,根据正方形的性质求解即可;
(2)分①当0<t≤3时,②当3<t≤5时,根据三角形的面积公式及二次函数的性质求解.
(1)(7,0)或(16,0)或(28,0)
提示:除已给图外还有两种情况,如下图.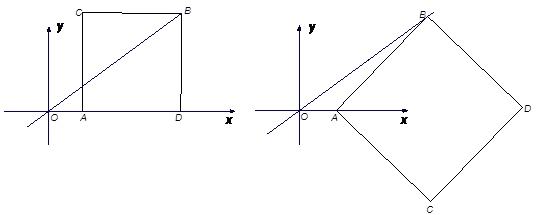
(2)①当0<t≤3时,过点P作PE⊥x轴,垂足为点E.
AQ=OP=t,OE=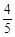 t,AE=4-
t,AE=4-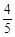 t.
t.
S△APQ=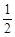 AQ·AE=
AQ·AE=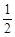 t(4-
t(4-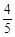 t)=
t)=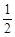 (t-
(t-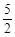 )2+
)2+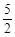
当t=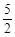 时,S△APQ的最大值为
时,S△APQ的最大值为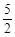 ;
;
②当3<t≤5时,过点P作PE⊥x轴,垂足为点E,过点Q作QF⊥x轴,垂足为点F
OP=t,PE=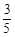 t,OE=
t,OE=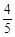 t,AE=4-
t,AE=4-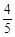 t.
t.
QF=3,AF=BQ=t-3,EF=AE+AF=1+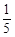 t
t
S△APQ="S" 梯形PEFQ-S△PEA-S△QFA=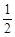 (PE+QF)·EF-
(PE+QF)·EF-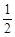 PE·AE-
PE·AE-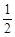 QF·AF
QF·AF
=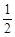 (
(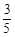 t +3)·(1+
t +3)·(1+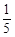 t)-
t)-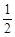 ·
·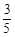 t·(4-
t·(4-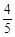 t)-
t)-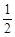 ×3·(t-3)=
×3·(t-3)=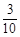 (t-
(t- )2+
)2+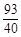
∵抛物线开口向上,
∴当t=5时,S△APQ的最大值为3>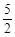
∴在移动过程中,△PAQ的面积最大值是3.
考点:动点问题的综合题
点评:此类问题难度较大,在中考中比较常见,一般在压轴题中出现,需特别注意.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
| m |
| x |
 )作x轴的平行线分别交双曲线y=
)作x轴的平行线分别交双曲线y=| m |
| x |
| m |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
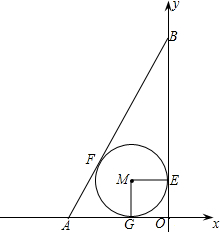 如图,已知直线l经过点D(-1,4),与x轴的负半轴和y轴的正半轴分别交于A,B两点,且直角△AOB的内切圆的面积为π,求直线l对应的一次函数的表达式.
如图,已知直线l经过点D(-1,4),与x轴的负半轴和y轴的正半轴分别交于A,B两点,且直角△AOB的内切圆的面积为π,求直线l对应的一次函数的表达式.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•奉贤区三模)如图,已知直线l经过点A(1,0),与双曲线y=
(2012•奉贤区三模)如图,已知直线l经过点A(1,0),与双曲线y=| m |
| x |
| m |
| x |
| m |
| x |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年山东临沂青云镇中心中学七年级下学期期末考试数学卷(带解析) 题型:单选题
如图,已知直线 ∥
∥ ,点
,点 在直线
在直线 上,且
上,且 ⊥
⊥ ,∠1=25°,则∠2的度数为
,∠1=25°,则∠2的度数为
| A.65° | B.25° | C.35° | D.45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com