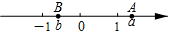练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．如图，A，B两点在数轴上表示的数分别是a，b，下列式子成立的是（　　）
    A．ab＞0B．a+b＞0C．（a-1）（b-1）＞0D．（a+1）（b-1）＞0

    分析 先根据数轴确定a，b的取值范围，再逐一判定即可解答．

    解答 解：由数轴可得：-1＜b＜0＜1＜a，
    ∴ab＜0，a+b＞0，（a-1）（b-1）＜0，（a+1）（b-1）＜0，
    故选：B．

    点评 本题考查了数轴，解决本题的关键是根据数轴确定a，b的取值范围．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    9．二次根式$\sqrt{-2x+4}$有意义，则实数x的取值范围是x≤2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如果（am•b•bn）3=a6b15，那么m=2，n=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，在△ABC中，点D在边BC上，且DC=2BD，点E是边AC的中点，设$\overrightarrow{BC}=\vec a，\overrightarrow{AC}=\vec b$，那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$；（用不$\vec a、\vec b$的线性组合表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

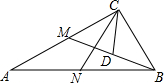    14．已知，在Rt△ABC中，∠ACB=90°，∠A=30°，点M、N分别是边AC、AB的中点，点D是线段BM的中点．
    （1）求证：$\frac{CN}{AB}=\frac{CD}{MB}$；
    （2）求∠NCD的余切值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

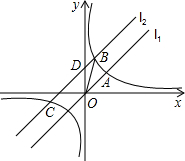    4．如图，直线l1：y=x与反比例函数$y=\frac{k}{x}$的图象c相交于点A（2，a），将直线l1向上平移3个单位长度得到l2，直线l2与c相交于B，C两点，（点B在第一象限），交y轴于点D．
    （1）求反比例函数的表达式并写出图象为l2的一次函数的表达式；
    （2）求B，C两点的坐标并求△BOD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．不等式组$\left\{\begin{array}{l}{\frac{1}{2}x+1≥-3}\\{x-2（x-3）＞0}\end{array}\right.$的解集是-8≤x＜6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

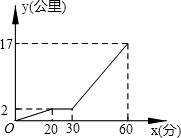    8．星期天下午，小强和小明相约在某公交车站一起乘车回学校，小强从家出发先步行到车站，等小明到了后两人一起乘公共汽车回到学校．图中折线表示小强离开家的路程y（公里）和所用的时间x（分）之间的函数关系．下列说法错误的是（　　）
    A．小强从家到公共汽车站步行了2千米
    B．小强在公共汽车站等小明用了10分钟
    C．公交车的平均速度是34千米/小时
    D．小强乘公交车用了30分钟

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：-（$\frac{1}{3}$）-1+（-1）0-|2-$\sqrt{12}$|．

    查看答案和解析>>

    同步练习册答案